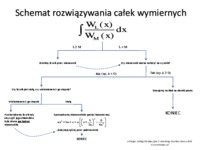
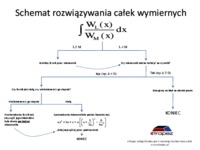
Równanie różniczkowe pierwszego rzędu - wykład
- Politechnika Wrocławska
- Analiza
RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU I. Równania o zmiennych rozdzielonych Przekształcamy tak, żeby uzyskać: związek z y dy związek z x dx / związek z y dy związek z x dx Rozwiązanie II. Równania typu y ' f ax by c Podstawiamy: t ax by ...