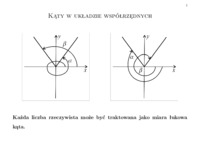
1 Miara łukowa kąta Definicja Miarą łukową kąta w kole o promieniu r nazywamy stosunek długości łuku, na którym oparty jest ten kąt, do długości promienia koła. Jednostką miary łukowej jest radian. 90 ◦ = 1 42 πr r rad = π 2 rad 180 ◦ =...
1 FUNKCJE f jest funkcj (odwzorowaniem) ze zbioru X w zbiór Y, je li f przyporz dkowuje ka demu elementowi ze zbioru X co najwy ej jeden element ze zbioru Y . ( ) Y y x f x X f Y X f ∈ = ∋ → : : Dziedzina funkcji: ( ) { } x f X x Df ∃ ∈ = : : Przeci...
Pojęcia topologiczne Granica funkcji i ciagu w przestrzeniach topologicznych i metrycznych Niech X ,Y - przestrzenie topologiczne, f : X Y x 0∈ ' D f ( x 0 - punkt sk...
1 Otoczenie i Sąsiedztwo Niech x 0 ∈ R oraz δ 0 . • Przedział ( x 0 − δ , x 0 + δ ) nazywamy otoczeniem punktu x0 o promieniu δ i oznaczamy U ( x 0 , δ ) . • Przedział x 0 , x 0 + δ ) nazywamy otoczeniem prawostronnym punktu x 0 o promieniu δ . • Przedział ( x 0 − δ...
1 Twierdzenie o całkowaniu przez cz ci ( ) I D g f ∈ , ( ) ( ) ( ) ( ) ( ) ( ) dx x g x f x g x f dx x g x f ′ − = ′ , I x ∈ o ile istniej całki po prawej i po lewej stronie równo ci. Dowód ( ) ( ) ( ( ) ( ) ( ) ( ) x g x f x g x f x g x f ′ + ′ = ′ całkuj c dwie strony ró...
1 RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ. Na potrzeby kolejnych twierdze /dowodów/itd. wprowadzam nast puj ce oznaczenie: I , J - dowolne przedziały. R I f → : R I F → : Funkcj F nazywamy funkcj pierwotn funkcji f , je li ( ) ( ) x f x F I x = ′ ∀ ∈ Obserwacja...
1 Pochodna logarytmiczna Wzór ( ln f ( x ) ) = f ( x ) f ( x ) nosi nazwę pochodnej logarytmicznej . Przykład Oblicz, używając pochodnej logarytmicznej, pochodne następujących funkcji: • f ( x ) = u ( x ) v ( x ) • f ( x ) = 3 x 3 · sin2 x √ x 2+1 2
1 Pochodna funkcji [ ] [ ] b a x b a D R R f f , , : 0 ∈ = → je eli ( ) ( ) 0 0 0 lim x x x f x f x x − − → ∃ , ( ) { } 0 \ , x b a x ∈ , to definiujemy pochodn funkcji f w punkcie x0 : ( ) ( ) ( ) 0 0 0 lim : 0 x x x f x f x x x f − − → = ′ ...
1 Pochodna funkcji Definicja Niech x 0 ∈ R oraz niech funkcja f będzie określona przynajmniej w pewnym otoczeniu punktu x 0 . Ponadto niech ∆ x będzie takie, że x = x 0 + ∆ x należy do tego otoczenia. • Liczbę ∆ x nazywamy wówczas przyrostem argumentu , a róznicę ∆ f = f ( x 0 + ∆ ...
ZASTOSOWANIA RACHUNKU POCHODNYCH: ALGORYTMÓW RÓŻNICZKOWANIA Równanie stycznej. Gdy badamy funkcje y = f ( x ), to równanie stycznej do wykresu tej funkcji w punkcie ( p, f ( p )) ma postać y − f ( p ) = f ( p )( x − p ) . Gdy krzywa jest określona w sposób parametryczny, tzn y = y ( t ...
