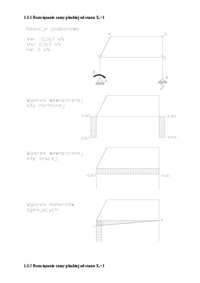
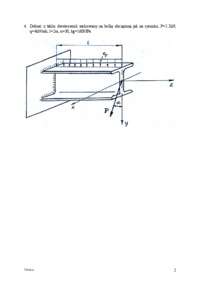
Rozkłady naprężeń normalnych
- Politechnika Śląska
- Mechanika budowli
Tematem jest rzeczywisty rozkład naprężeń normalnych w przekrojach pryzmatycznego pręta, osłabionego otworem oraz karbem, dla przypadków osiowego rozciągania oraz równomiernego zginania. Pojęcie współczynnika koncentracji naprężeń. Notatki zawierają wszystkie niezbędne rysunki oraz wzory wraz z obj...