WYKŁAD 3_1
1.PRZEMIANY pVT gazu doskonałego –w zakresie I zasady termodynamiki
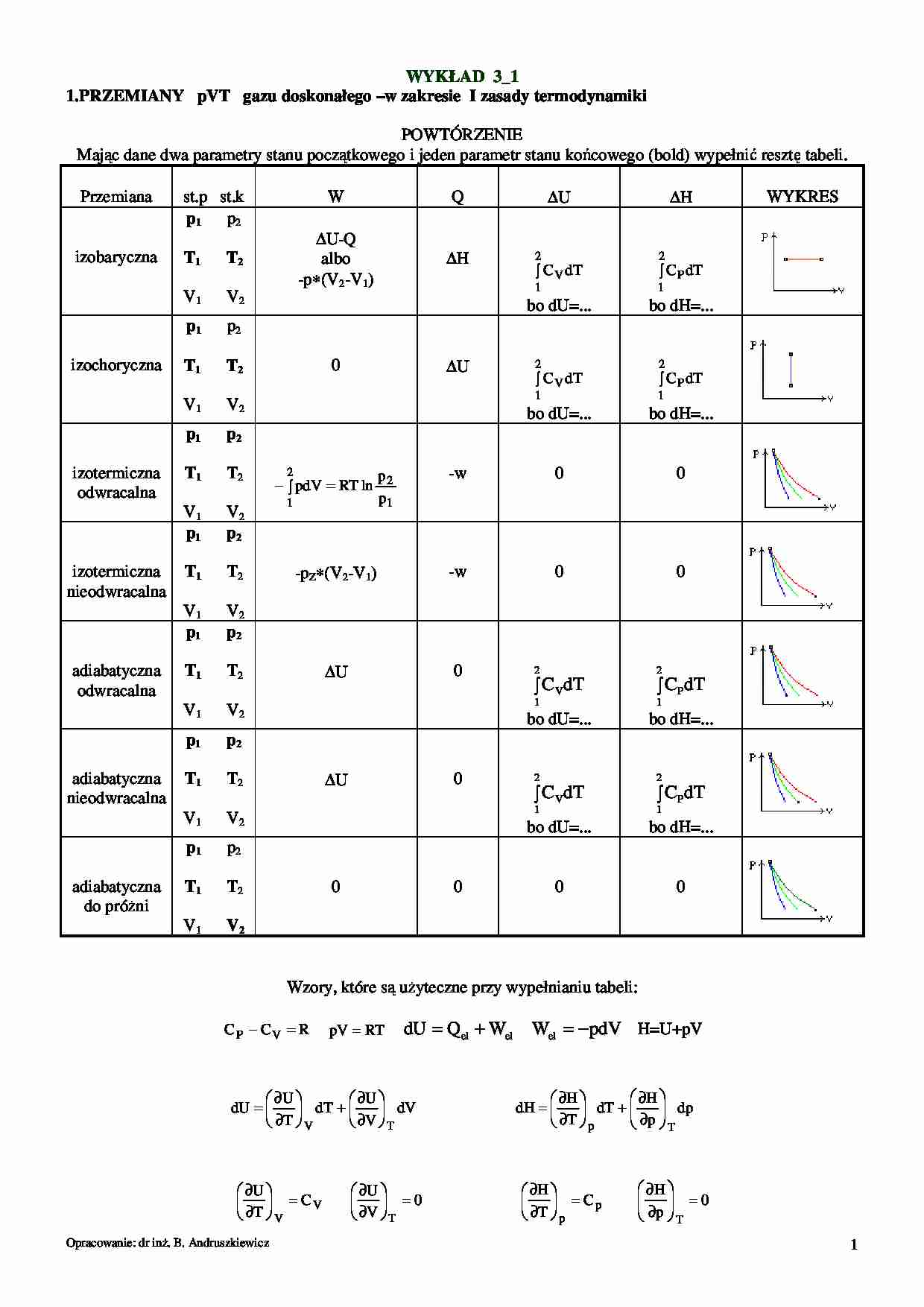
POWTÓRZENIE
Mając dane dwa parametry stanu początkowego i jeden parametr stanu końcowego (bold) wypełnić resztę tabeli.
Przemiana
izobaryczna
st.p st.k
p1
p2
T1
T2
V1
T1
T2
V2
p2
T1
T2
V1
p1
adiabatyczna
odwracalna
T1
2
2
∫ C V dT
∫ C P dT
1
T2
1
bo dH=...
-w
0
0
-pZ∗(V2-V1)
-w
0
0
∆U
0
2
− ∫ pdV = RT ln
1
p2
p1
2
1
T2
2
1
∫ C V dT
∫ C P dT
p2
T1
bo dU=...
V2
p1
V1
0
2
2
1
T2
V1
∆U
bo dH=...
1
∫ C V dT
∫ C P dT
p2
T1
bo dU=...
V2
p1
adiabatyczna
do próŜni
∆U
0
bo dH=...
V2
p2
V1
adiabatyczna
nieodwracalna
∫ C P dT
1
p2
V1
p1
izotermiczna
nieodwracalna
2
∫ C V dT
bo dU=...
V2
p1
izotermiczna
odwracalna
2
WYKRES
p2
T1
∆H
1
V2
p1
∆H
∆U
Q
∆U-Q
albo
-p∗(V2-V1)
T2
V1
izochoryczna
W
V2
bo dU=...
0
0
bo dH=...
0
0
Wzory, które są uŜyteczne przy wypełnianiu tabeli:
CP − CV = R
pV = RT
dU = Qel + Wel
∂U
∂U
dU =
dT +
dV
∂T V
∂V T
∂U
= CV
∂T V
Opracowanie: dr inŜ. B. Andruszkiewicz
∂U
=0
∂V T
Wel = − pdV H=U+pV
∂H
∂H
dH =
dT +
∂p dp
∂T p
T
∂H
= Cp
∂T p
∂H
∂p = 0
T
1
Obliczenie parametrów stanu końcowego adiabaty odwracalnej.
Dane – p1 , T1 , V1 , p2 . Szukane – T2 , V2 .
p1V1κ
p
⇒ V2 = V1 ∗ 1
p
2
κ
= p 2 V2
1/ κ
p 2 V2 = RT2 ⇒ T2 =
p 2 V2
gdzie κ=CP /CV
R
albo
C P dT = Vdp
C P ln
T2
p
= R ln 2 ⇒ T2 =
T1
p1
a później p 2 V2 = RT2 ⇒ V2 =
RT2
p2
Dane – p1 , T1 , V1 , V2 . Szukane – T2 , p2 .
p1V1κ
κ
= p 2 V2
V
⇒ p 2 = p1 ∗ 1
V
2
κ
p 2 V2 = RT2 ⇒ T2 =
p 2 V2
gdzie κ=CP /CV
R
albo
C V dT = −pdV
T
V
C V ln 2 = −R ln 2 ⇒ T2 =
T1
V1
a później p 2 V2 = RT2 ⇒ p 2 =
RT2
V2
Obliczenie parametrów stanu końcowego adiabaty nieodwracalnej.
Dane – p1 , T1 , V1 , p2 . Szukane – T2 , V2 .
− pdV = w el = dU = C V dT bo w przemianie adiabatycznej Qel =0
− p 2 ∗ (V2 − V1 ) = C V ∗ (T2 − T1 ) gdy ciśnienie zewnętrzne jest stałe i równe ciśnieniu
końcowemu.
RT
− p 2 ∗ 2 − V1 = C V ∗ (T2 − T1 )
bo dla gazu doskonałego V=RT/p
p
2
C T + p 2 V1 C V T1 + p 2 V1
=
− RT2 − C V T2 = −C V T1 − p 2 V1 ⇒ T2 = V 1
bo dla gazu doskonałego CP –CV =R
CV + R
CP
Parametry stanu końcowego adiabatycznego rozpręŜania do próŜni.
w el = −p z dV = 0 bo ciśnienie
zewnętrzne jest zerem; Q el = 0 bo
adiabatycznie; wobec tych dwu
przesłanek i I zasady termodynamiki
∆U = 0 .
PoniewaŜ dla gazu doskonałego U jest
funkcją tylko temperatury,
to T=const i dT=0,
a z tego następnie wynika, Ŝe ∆H = 0
oraz p1V1 = RT = p 2 V2
2. PRZEMIANY pVT gazu doskonałego –w zakresie II zasady termodynamiki
Przykład 1.
Obliczyć ∆S, gdy 1 mol gazu (p1 =1atm, T1 =300K, CP =30J/molK) rozpręŜa się izotermicznie odwracalnie do
ciśnienia końcowego p2=0,3atm. p1=1atm
p2=0,3atm
T1=300K
T2=300K
V1 =
RT1 8,314J ∗ 300K ∗ m 2
RT
m3
8,314J ∗ 300K ∗ m 2
m3
=
= 0,0246
; V2 = 2 =
= 0,08205
p1
mol ∗
(…)
… jest w czasie przemiany stałe i wynosi p2.
p2=0,3atm
p1=1atm
T1=300K
T2=300K
V1 =
RT1 8,314J ∗ 300K ∗ m 2
RT
m3
8,314J ∗ 300K ∗ m 2
m3
=
= 0,0246
; V2 = 2 =
= 0,08205
p1
mol ∗ K ∗ 101325N
mol
p2
mol ∗ K ∗ 101325N ∗ 0,3
mol
Ze względu na identyczność parametrów początkowych i końcowych tej nieodwracalnej przemiany
i przemiany z przykładu 1 ∆S musi tutaj równać się 10,01J/molK, bo entropia jest funkcją stanu.
Q…
… tego przenieść wartości ∆S=0 właściwej dla adiabaty odwracalnej na adiabatę nieodwracalną.
a)Pierwsza zastępcza droga przemiany wymyślona w celach obliczeniowych składa się z 2 etapów:
1mol(p1, T1,V1) →1mol(p2, T1,V’) →1mol(p2, T2,V2)
etap 1 - p.izotermicza; etap 2 - p.izobaryczna
Całkowita zmiana entropii jest sumą zmian w tych dwu etapach, bo entropia jest funkcją stanu.
2 ∂S
2 ∂S
2 − R
2C
p2
T2
P…
… być i dodatnia i ujemna.
Miarą nieodwracalności jest dodatni element ∆iS dodany do ułamka Q/T
8. Reakcje chemiczne i ich samorzutność.
(
)
(
∆G 0 = ∑ ν i ∆G 0 − ∑ ν j ∆G 0
twi
twj
prod
substr
)
Standardowy potencjał termodynamiczny reakcji jest algebraiczną sumą standardowych potencjałów
termodynamicznych tworzenia reagentów. Standardowość (0) oznacza oddzielne czyste reagenty
- a nie w postaci roztworów…
... zobacz całą notatkę





Komentarze użytkowników (0)