WYKŁAD 3_2
1.Relacje ciepło-praca w cyklach przemian ( przykład z „Obliczenia Fizykochemiczne” J.Pigoniowej).
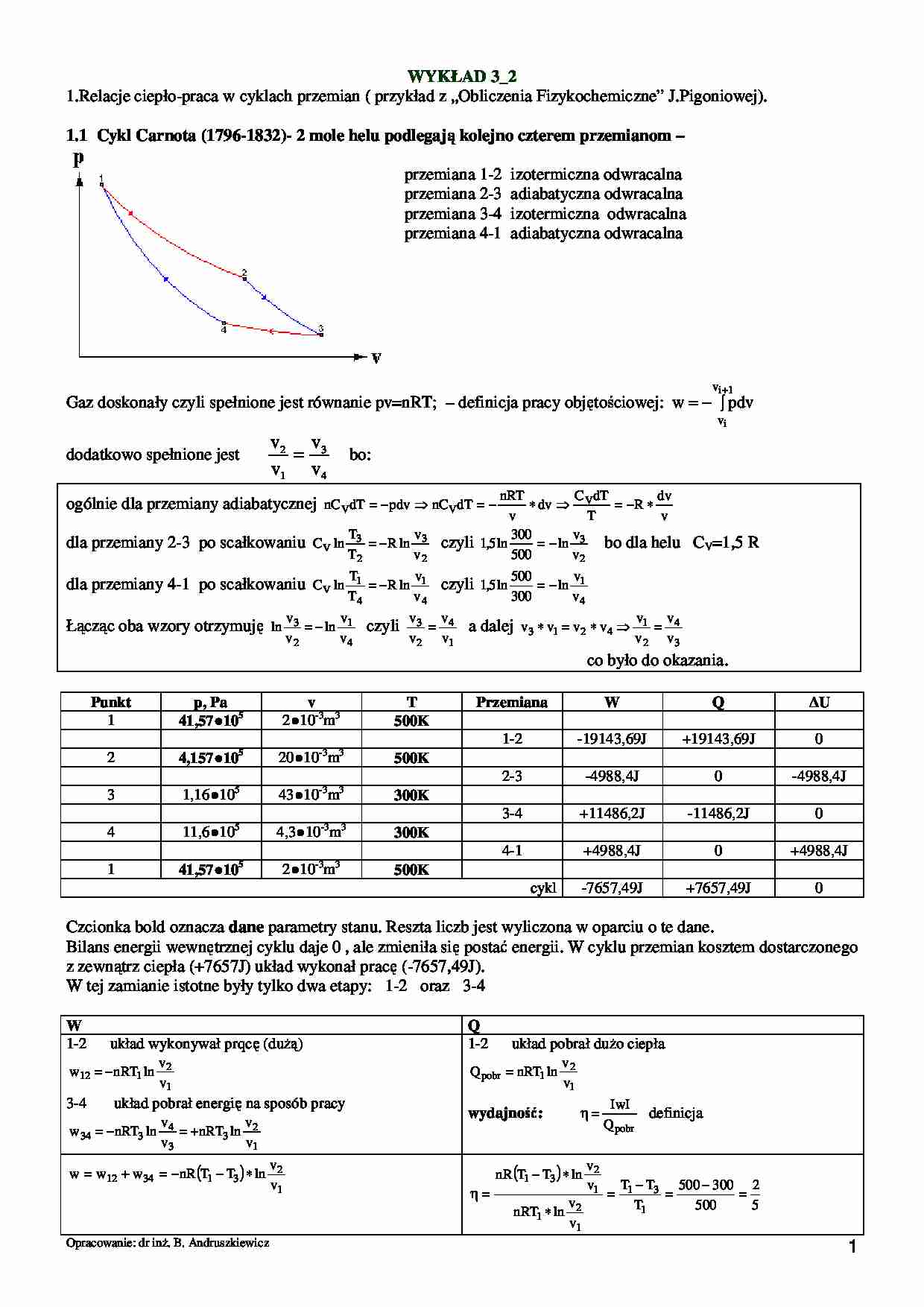
1.1 Cykl Carnota (1796-1832)- 2 mole helu podlegają kolejno czterem przemianom –
przemiana 1-2
przemiana 2-3
przemiana 3-4
przemiana 4-1
izotermiczna odwracalna
adiabatyczna odwracalna
izotermiczna odwracalna
adiabatyczna odwracalna
vi +1
Gaz doskonały czyli spełnione jest równanie pv=nRT; – definicja pracy objętościowej: w = − ∫ pdv
vi
dodatkowo spełnione jest
v 2 v3
=
v1 v 4
bo:
nRT
C dT
dv
∗ dv ⇒ V
= −R ∗
v
T
v
300
v3
1,5 ln
= − ln
bo dla helu
500
v2
ogólnie dla przemiany adiabatycznej nCV dT = − pdv ⇒ nCV dT = −
dla przemiany 2-3 po scałkowaniu C V ln
T3
v
= − R ln 3
T2
v2
czyli
dla przemiany 4-1 po scałkowaniu C V ln
T1
v
= − R ln 1
T4
v4
czyli 1,5 ln
v3
v
= − ln 1
v2
v4
Łącząc oba wzory otrzymuję ln
czyli
v3 v 4
=
v 2 v1
CV=1,5 R
500
v
= − ln 1
300
v4
a dalej v3 ∗ v1 = v 2 ∗ v 4 ⇒
v1 v 4
=
v 2 v3
co było do okazania.
Punkt
1
p, Pa
41,57●105
v
2●10-3m3
T
500K
2
4,157●105
20●10-3m3
500K
3
1,16●105
43●10-3m3
300K
4
11,6●105
4,3●10-3m3
300K
1
41,57●105
2●10-3m3
Przemiana
W
Q
∆U
1-2
-19143,69J
+19143,69J
0
2-3
-4988,4J
0
-4988,4J
3-4
+11486,2J
-11486,2J
0
500K
4-1
+4988,4J
0
+4988,4J
-7657,49J
+7657,49J
0
cykl
Czcionka bold oznacza dane parametry stanu. Reszta liczb jest wyliczona w oparciu o te dane.
Bilans energii wewnętrznej cyklu daje 0 , ale zmieniła się postać energii. W cyklu przemian kosztem dostarczonego
z zewnątrz ciepła (+7657J) układ wykonał pracę (-7657,49J).
W tej zamianie istotne były tylko dwa etapy: 1-2 oraz 3-4
W
1-2
w12
3-4
w 34
układ wykonywał prqcę (duŜą)
v
= − nRT1 ln 2
v1
v
v
= − nRT3 ln 4 = + nRT3 ln 2
v3
v1
Opracowanie: dr inŜ. B. Andruszkiewicz
układ pobrał duŜo ciepła
Q pobr = nRT1 ln
układ pobrał energię na sposób pracy
w = w12 + w 34 = −nR (T1 − T3 ) ∗ ln
Q
1-2
v2
v1
wydajność:
η=
v2
v1
η=
nR (T1 − T3 ) ∗ ln
v
nRT1 ∗ ln 2
v1
v2
v1
IwI
Q pobr
=
definicja
T1 − T3 500 − 300 2
=
=
T1
500
5
1
Kelvin: W procesie kołowym nie jest moŜliwe pobranie ciepła ze źródła i zamiana go w pracę ( w całości ) bez
jednoczesnego przeniesienia ciepła ze źródła (500K) do chłodnicy (300K).
1.2 Odwrotny cykl Carnota (lodówka)- 2 mole helu - gaz doskonały
przemiana 1-4
przemiana 4-3
przemiana 3-2
przemiana 2-1
adiabatyczna odwracalna
izotermiczna odwracalna
adiabatyczna odwracalna
izotermiczna odwracalna
vi +1
Gaz doskonały czyli spełnione jest równanie pv=nRT; – definicja pracy objętościowej: w = − ∫ pdv
vi
dodatkowo spełnione jest
v 2 v3
=
v1 v 4
jak wykazałam poprzednio.
Punkt
1
p, Pa
41,57●105
v
2●10-3m3
T
500K
4
11,6●105
4,3●10-3m3
300K
3
1,16●105
43●10-3m3
300K
2
4,157●105
20●10-3m3
500K
1
41,57●105
2●10-3m3
Przemiana
W
Q
∆U
1-4
-4988,4J
0
-4988,4J
4-3
-11486,2J
+11486,2J
0
3-2
+4988,4J
0
+4988,4J
500K
2-1
+19143,69J
-19143,69J
0
+7657,49J
-7657,49J
0
cykl
Czcionka bold oznacza dane parametry
(…)
…
izochorycznie - izotermicznie ) :
dF = - TdiS czyli dla 1 mola ∆F = - ∆i S•T
•
∆F<0 tzn, Ŝe reakcja nieodwracalnie czyli samorzutnie biegnie od substratów do produktów.
∆F>0 tzn, Ŝe reakcja nie przebiegnie od substratów do produktów. tylko odwrotnie. Substraty mają
mniejsze F, są korzystniejsze.
∆F=0 to znaczy, Ŝe nie ma powodu do Ŝadnych zmian - równowaga.
3.3 W przemianach fazowych parametry stanu p i T…
... zobacz całą notatkę





Komentarze użytkowników (0)