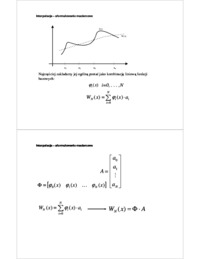
Omówienie zagadnień metod numerycznych.
- Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie
- Wykłady monograficzne
Metody Numeryczne II rok II rok Informatyka Stosowana Metody numeryczne 1. Błędy w obliczeniach numerycznych. 2. Rozwiązywanie układów równań liniowych • metoda eliminacji Gaussa – Jordana i Gaussa • metody dekompozycji (LU) 3. Int...