Zadanie 1
Na podstawie Rocznika Statystycznego dobierz dwie serie danych do analizy poziomu średniego zmiennych, rozrzutu względem średniej oraz liniowej zależności jednej zmiennej od drugiej. Dane powinny być zebrane z minimum 20 okresów (stanów zmiennej). Dokonaj wizualizacji danych oraz przedstaw wyniki analiz w postaci wykresów.
Dobór danych.
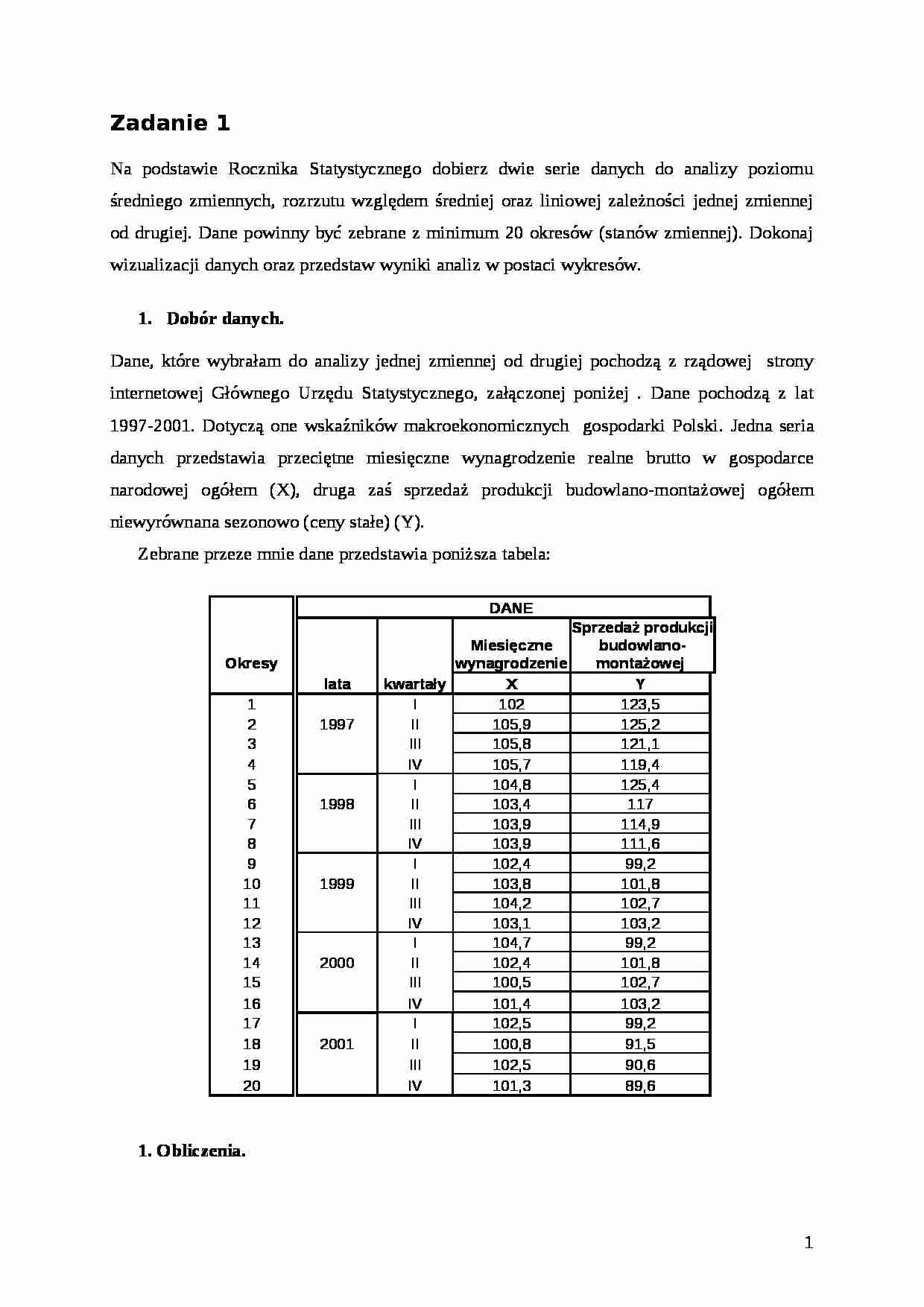
Dane, które wybrałam do analizy jednej zmiennej od drugiej pochodzą z rządowej strony internetowej Głównego Urzędu Statystycznego, załączonej poniżej . Dane pochodzą z lat 1997-2001. Dotyczą one wskaźników makroekonomicznych gospodarki Polski. Jedna seria danych przedstawia przeciętne miesięczne wynagrodzenie realne brutto w gospodarce narodowej ogółem (X), druga zaś sprzedaż produkcji budowlano-montażowej ogółemniewyrównana sezonowo (ceny stałe) (Y). Zebrane przeze mnie dane przedstawia poniższa tabela:
DANE
Okresy
lata
kwartały
Miesięczne wynagrodzenie
Sprzedaż produkcji budowlano- montażowej X
Y
1
I
102
123,5
2
1997
II
105,9
125,2
3
III
105,8
121,1
4
IV
105,7
119,4
5
I
104,8
125,4
6
1998
II
103,4
117
7
III
103,9
114,9
8
IV
103,9
111,6
9
I
102,4
99,2
10
1999
II
103,8
101,8
11
III
104,2
102,7
12
IV
103,1
103,2
13
I
104,7
(…)
… kryterium klasyfikacji (prognoza ze względu na cel lub funkcję). W podanych prognozach wskaż obiekt, zjawisko, zmienną.
Podaj, na podstawie Rocznika Statystycznego, przykłady:
wielowymiarowego szeregu czasowego
wielowymiarowego szeregu przekrojowego
szeregu przekrojowo-czasowego
1. Do przykładów swoich prognoz zastosowałam kryterium ze względu na cel lub funkcję.
Przykłady prognoz:
prognoza preparacyjna…
… komputerowe. obiekt
zjawisko
zmienna
Polska
Spadek cen mikroprocesorów
mierzalna
Treść prognozy: W 2020 r. zwiększy się dziura ozonowa, w związku z czym zwiększy się popyt na kremy z filtrem przeciwko UV.
obiekt
zjawisko
zmienna
Świat Zwiększenie dziury ozonowej
niemierzalna
prognoza badawcza Treść prognozy: W 2006 roku Polska przystąpi do UE w związku z czym Polacy częściej będą odwiedzać kraje europejskie…
… Przykłady szeregów :
wielowymiarowego szeregu czasowego:
Lata
Uczniowie szkół podstawowych
(tys.)
Uczniowie szkół ogólnokształcących
(tys.)
Uczniowie szkół ogólnokształcących
(tys.)
Uczniowie szkół zawodowych
(tys.)
1990
5287,0
445,0
1451,1
814,5
1991
5310,5
499,8
1477,9
806,2
1992
5312,6
555,8
1502,0
792,8
1993
5278,4
602,4
1534,1
769,5
Źródło: Rocznik statystyczny Polska w latach 1946-1994 ( załączone…
…. analizowanego zjawiska gospodarczego z okresu poprzedniego zbuduj prognozę badanej wielkości na jeden krok naprzód. Do budowy prognozy należy wykorzystać proste metody prognozowania na podstawie szeregów czasowych:
metoda naiwna,
metoda średniej ruchomej,
metoda wygładzania wykładniczego prostego.
Cel prognozy, wybór postawy, podanie przesłanek prognostycznych.
Zebrane przeze mnie dane pochodzą ze strony…
…
306,867
478,600
443,756
Z przeprowadzonej analizy wynika, iż najlepszą metodą prognozowania dla przedstawionych danych jest metoda średniej ruchomej przy stałej wygładzania k równej 5. Prognoza wyznaczona z wykorzystaniem tej metody jest obarczona najmniejszym spośród wszystkich przedstawionych metod błędem względnym prognozy 26,38 % oraz średnim błędem kwadratowym 90404,73 . Wartość S* jest w związku…
…. w województwie podlaskim zwiększy się ilość zwierząt chorych na wściekliznę obiekt
zjawisko
zmienna
Woj. podlaskie
wzrost ilości zwierząt chorych na wściekliznę mierzalna
Treść prognozy: W listopadzie 2003 r. na obszarze północno-wschodniej Polski spadnie pierwszy śnieg
obiekt
zjawisko
zmienna
Północno-wschodnia Polska
Opad pierwszego śniegu
niemierzalna
f) prognoza aktywna Treść prognozy: W XII br. wzrośnie…
... zobacz całą notatkę





Komentarze użytkowników (0)