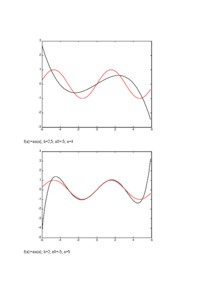
Rozwiązywanie równań nieliniowych - omówienie
- Politechnika Warszawska
- Metody numeryczne
W1/2 str 1 Rozwi zywanie równa nieliniowych Niech f b dzie funkcj okre lon na przedziale [a,b]. Zadaniem jest znalezienie takiego α z tego przedziału, e f (α) = 0. Oczywi cie takich warto ci α mo e by wiele. Numerycznie, takie zadanie, rozwi zuje si zwykle metodami iteracyjnymi, tj. tworzymy ...