To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
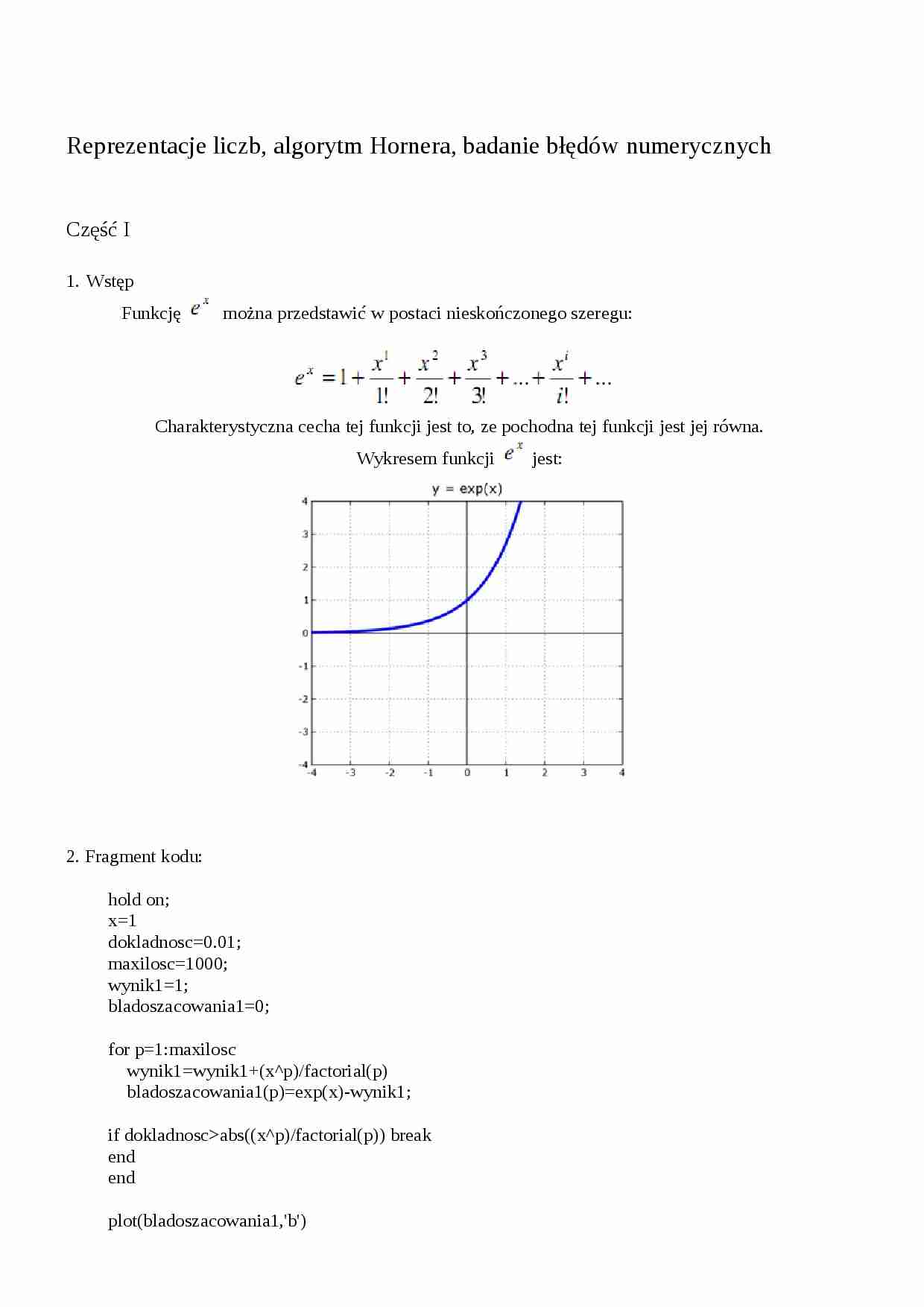


Reprezentacje liczb, algorytm Hornera, badanie błędów numerycznych Część I 1. Wstęp Funkcję można przedstawić w postaci nieskończonego szeregu:
Charakterystyczna cecha tej funkcji jest to, ze pochodna tej funkcji jest jej równa. Wykresem funkcji jest: 2. Fragment kodu: hold on;
x=1
dokladnosc=0.01;
maxilosc=1000; wynik1=1;
bladoszacowania1=0;
for p=1:maxilosc
wynik1=wynik1+(x^p)/factorial(p)
bladoszacowania1(p)=exp(x)-wynik1;
if dokladnoscabs((x^p)/factorial(p)) break
end
end
plot(bladoszacowania1,'b')
Wykres po zaimplementowaniu kodu programu: 3. Podsumowanie Program został napisany w środowisku Matlab. Było to pierwsze nasze zetknięcie się z tym środowiskiem programistycznym, wiec jeśli wystąpił jakiś błąd był on spowodowany jedynie niewiedzą studentów na temat środowiska programistycznego. Po zaimplementowaniu kodu programu i z wyrysowanego przez niego wykresu możemy stwierdzić, iż wszystkie błędy dążą do „0”, więc jest to jak najbardziej wskazane zachowanie. Możemy również zaobserwować, iż po każdym przejściu przez pętlę for błąd zmniejsza się, gdyż dodawane są coraz dokładniejsze przybliżenia. Część II 1. Wstęp Dowolny wielomian o postaci:
mona zapisać w postaci, która pozwala na realizację tzw. algorytmu Hornera:
Kolejno definiujemy: Podstawiamy bn do wielomianu:
2. Fragment kodu float liczenie() {
cout n; for (int i = 0; i tab_a[i];
}
cout x;
float wynik = tab_a[n];
for (int i = n - 1; i = 0; i--) {
wynik = wynik * x + tab_a[i];
}
return wynik;
}
3. Podsumowanie Przy wykorzystaniu algorytmów "mnożących" takich jak algorytm Hornera skracamy diametralnie czas wykonywania, rozwiązywania zadania poprzez znaczne ograniczenie czynności mnożenia, która jest bardzo czasochłonna. Przykładowo dla wielomianu stopnia 3 przy tradycyjnym rozwiązaniu wykonujemy aź 6 mnożeń, podczas gdy przy użyciu algorytmu Hornera tylko 3 to skraca czas obliczeń, zważywszy na to, że ilość poszczególnych operacji dodawania jest niezmienna.
Część III 1. Wstęp Przedstawienie liczby w postaci binarnej, znaczy zapisanie jej w formacie „0” i „1”. W komputerze, każda informacja musi mieć postać ciągu zer i jedynek, dlatego znak liczby jest reprezentowany przez dodatkową cyfrę dwójkową, zwaną bitem znaku, która poprzedza właściwe cyfry liczby. Cyfra „l” na pozycji bitu znaku zastępuje tradycyjny znak minus w zapisie liczb ujemnych, a „0” występuje zawsze przed liczbami nieujemnymi. Bitu znaku liczby w reprezentacji binarnej nie można pominąć.
(…)
… to: ";
if (liczba > 0)
{
cout << "0.";
binarnie(liczba);
}
if (liczba < 0)
{
cout << "1." ;
liczba = liczba *(-1);
binarnie(liczba);
} 3. Podsumowanie Celem ćwiczenia było zapoznanie się z zapisywaniem cyfr w formacie binarnym oraz zaimplementowanie tych wiadomości w kodzie źródłowym programu. Liczbę ujemną możemy zapisać na kilka sposobów:
- znak-moduł 5 = 0101 -5 = 1101 - dopełnienie do jedynki…
... zobacz całą notatkę






Komentarze użytkowników (0)