Geodezja wyższa i astronomia geodezyjna

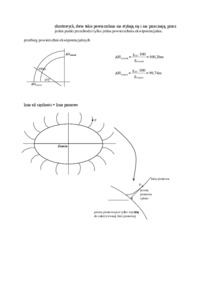
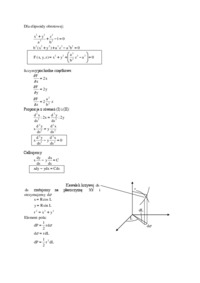
GEODEZJA FIZYCZNA ELEMENTÓW Elementy geodezji dynamicznej. m1  m2 r2 Przyspieszenie siły przyciągania, siły ciężkości i odśrodkowej: 1 gal  1cm  s 2 Prawo Newtona (o wzajemnym przyciąganiu): F  k  m 1miligal  10 3 cm  s 2 1mikrogal  10 6 cm  s 2 R M Ziemia - siła przyciąg...

GEOMETRIA ELIPSOIDY OBROTOWEJ ab 1 , dla Ziemi p  a 298,257 2 2 1 a b I mimośród e: e 2  , e 2 12 a 2 2 a b II mimośród e': e' 2  b2 Aby określić elipsoidę obrotową wystarczy znać dwie z następujących wielkości: a, b, p, e2, e'2 Oficjalnie a  6378,137km  1m ale właści...

Trzy główne przyczyny wpływają na zmianę wartości g na powierzchni Ziemi: 1. przyśpieszenie odśrodkowe, 2. spłaszczenie Ziemi (odległość od środka masy M), 3. rozkład gęstości mas w skorupie ziemskiej. Inne przyczyny to czynniki zmienne (przyciąganie Słońca, Księżyca, planet i skład grawimetry...

HIPOTEZY IZOSTAZJI 1. Pratt (Hayforda) (1855) „różne gęstości dla różnych wysokości słupów” geoida 100 – 110 km powierzchnia izostatyczna (równowaga hydrostatyczna) 2. Airy Heisanen (1856) SiAl geoida SiMa 100 – 110 km powierzchnia izost...

KRZYWIZNA LINII NA POWIERZCHNI, TWIERDZENIA MEUSNIERA I EULERA. Krzywa przechodzi przez punkt P i leży na powierzchni, więc można powiedzieć, że powstała przez przecięcie powierzchni z płaszczyzną (a przynajmniej każdy nieskończenie mał...

LINIA GEODEZYJNA (ORTODROMA) Taka krzywa na powierzchni, która: - jest najkrótszą odległością między dwoma punktami na powierzchni - gdyby na punkt poruszający się po powierzchni ni...

NIWELACJA ASTRONOMICZNA Pozwala wyznaczyć odstępy geoidy od elipsoidy gdy znane są względne odchylenia pionu. W tym celu obserwuje się  i  na punktach, gdzie B i L znane są z pomiarów geodezyjnych. Mając parami współrzędne na tych samych punktach (astronomiczne i geodezyjne) można obliczyć sk...

NIWELACJA PRECYZYJNA Systemy wysokościowe precyzyjnej niwelacji geometrycznej. W=WB B dh W=Wi+dW g W=Wi A W=WA potencjał poziom geoidy W=W0 Zmiana potencjału W o dW wiąże się ze zmianą wysokości H o dh. dW dW   g  dh  g czyli dh gdzie: W – potencjał siły ciężkości h – kier...

OBLICZENIE DŁUGOŚCI ŁUKU POŁUDNIKA dS  MdB P2 n 2 dS P n1 1 B2 S   MdB  B2  a(1  e 2 ) 3 dB (1  e sin B) Jest to wzór ścisły umożliwiający obliczenie długości łuku południka o dowolnej długości. Ponieważ jednak jest to c...

ODWZOROWANIE GAUSSA – KRUGERA (zwane w krajach anglosaskich poprzecznym odwzorowaniem Merkatora) I. ( B, L)  ( x' , y' ) wiernokątnie e   B   1  e sin B  2 x'  a ln tg        4 2   1  e sin B  y  aL L  L  L0 L0 - długość pewnego