To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Trzy główne przyczyny wpływają na zmianę wartości g na powierzchni Ziemi:
1. przyśpieszenie odśrodkowe,
2. spłaszczenie Ziemi (odległość od środka masy M),
3. rozkład gęstości mas w skorupie ziemskiej.
Inne przyczyny to czynniki zmienne (przyciąganie Słońca, Księżyca, planet i skład
grawimetryczny planet).
Przesunięcie jednorodnej masy kulistej m o dr wbrew sile przyciągania w polu działania siły o
masie M wymaga elementarnej pracy dL:
r
dr
M
m
dL F dr
Mm
dr /
r2
dr
L kMm 2
r
dla _ dr
dL k
dr
1
1
L kMm 2 kMm
kMm V m
rr
r
r
r
M
- potencjał siły przyciągania
V k
r
Potencjał siły odśrodkowej:
Praca wykonana w płaszczyźnie równoleżnika przez siłę odśrodkową f wynosi:
m 2 2
dL f d m 2 d L
U m
2
2 2 2 x2 y2
U
- potencjał siły odśrodkowej
2
2
Potencjał siły ciężkości nazywamy funkcją W
M 2 2
W V U k
r
2
dW
M
k 2 2 g
dr
r
( porównaj z równaniem *)
Powierzchnie ekwipotencjalne (jednakowego potencjału):
1
W x, y, z V x, y, z 2 x 2 y 2 const
2
W x, y, z Co
- geoida, zawiera w sobie powierzchnię mórz i oceanów, przebieg
powierzchni ekwipotencjalnych bliska Ziemi jest podobny do elipsoid
obrotowych, dwie takie powierzchnie nie stykają się i nie przecinają, przez
jeden punkt przechodzi tylko jedna powierzchnia ekwipotencjalna.
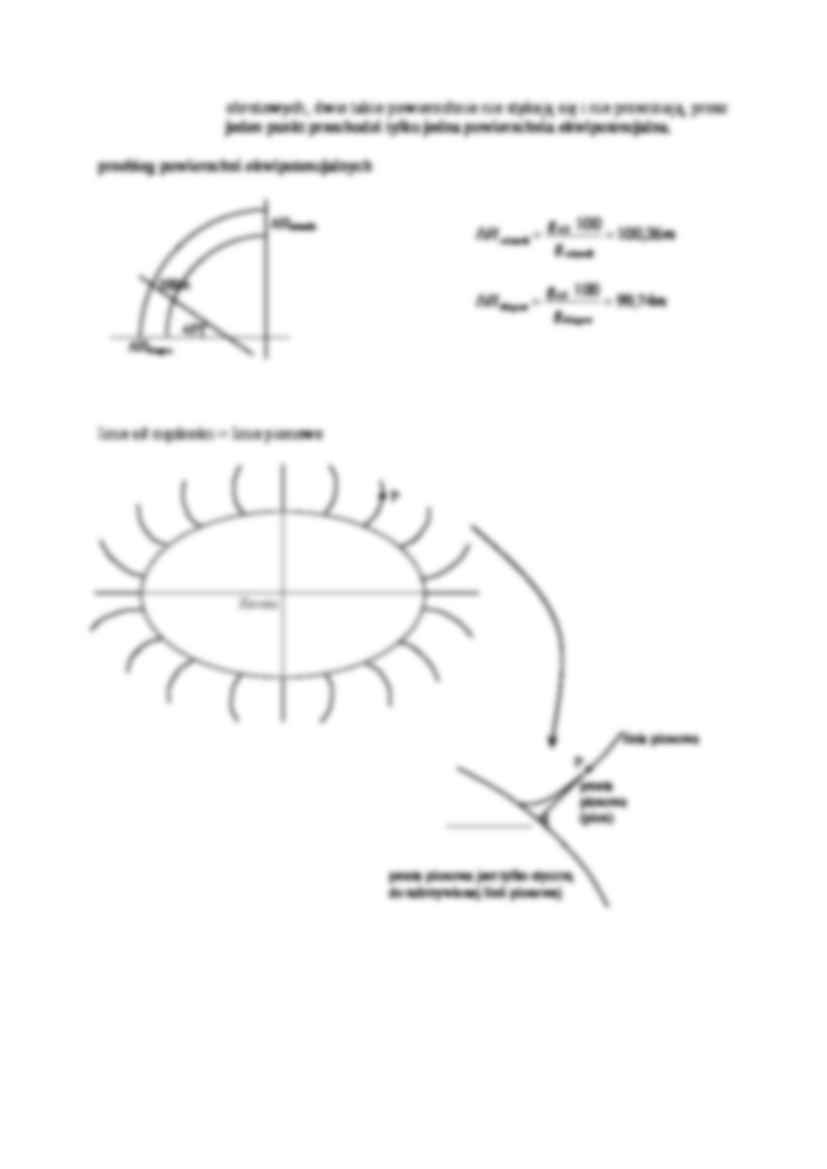
przebieg powierzchni ekwipotencjalnych
H równik
100m
45o
g 45 100
100,26m
g równik
H biegun
Hrównik
g 45 100
99,74m
g biegun
Hbiegun
linie sił ciężkości = linie pionowe
P
Ziemia
linia pionowa
P
prosta
pionowa
(pion)
prosta pionowa jest tylko styczną
do zakrzywionej linii pionowej
Własność powierzchni ekwipotencjalnej:
- są to powierzchnie obrotowe, gdzie osią obrotu jest oś Ziemi;
- w pobliżu Ziemi są to powierzchnie zamknięte, ciągłe zbliżone do elipsoid obrotowych lub
dalej od Ziemi rozciągające się do powierzchnie walcowe;
- przyspieszenie g jest na powierzchni ekwipotencjalnej najmniejsze na równiku, największe
na biegunie;
- gdy g0 istnieje tylko jedna normalna linia pionowa do powierzchni ekwipotencjalnej;
- są powierzchniami nierównoległymi, odstępy są większe w pobliżu równika;
2
- w odległości 6 R zachodzi g’= -c czyli g=0.
3
2
6 R
3
R
g=0
Przyśpieszenie siły ciężkości – wzory, pomiary, redukcje.
Wzór Clairaulta.
lub
g g a 1 sin 2 sin2 2
g g a 1 sin 2
przyśpieszenie
na Ziemi
w punkcie
pod szerokością
geograficzną
przyśpieszenie
siły
ciężkości
na równiku
spłaszczenie
grawimetryc
zne
na biegunie
gb g a
ga
Wyznaczenie ga i :
w n punktach o znanym wyznaczamy g:
g1 g a 1 sin 2 1
n równań dla 2 niewiadomych (ga i )
g1 g a 1 sin 2 n
g – wynik pomiaru przyśpieszenia siły ciężkości
- oznaczenie przyśpieszenia normalnego, teoretyczne, obliczone ze wzorów typu Clairaulta
dla ziemi zregularyzowanej (przyjmując pewien rozkład mas i pewną figurę Ziemi)
... zobacz całą notatkę






Komentarze użytkowników (0)