Hipotezy izostazji- opracowanie

Nasza ocena:

5
Pobrań: 133
Wyświetleń: 1169
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
Hipotezy izostazji- opracowanie - strona 1 Hipotezy izostazji- opracowanie - strona 2 Hipotezy izostazji- opracowanie - strona 3

Fragment notatki:

HIPOTEZY IZOSTAZJI
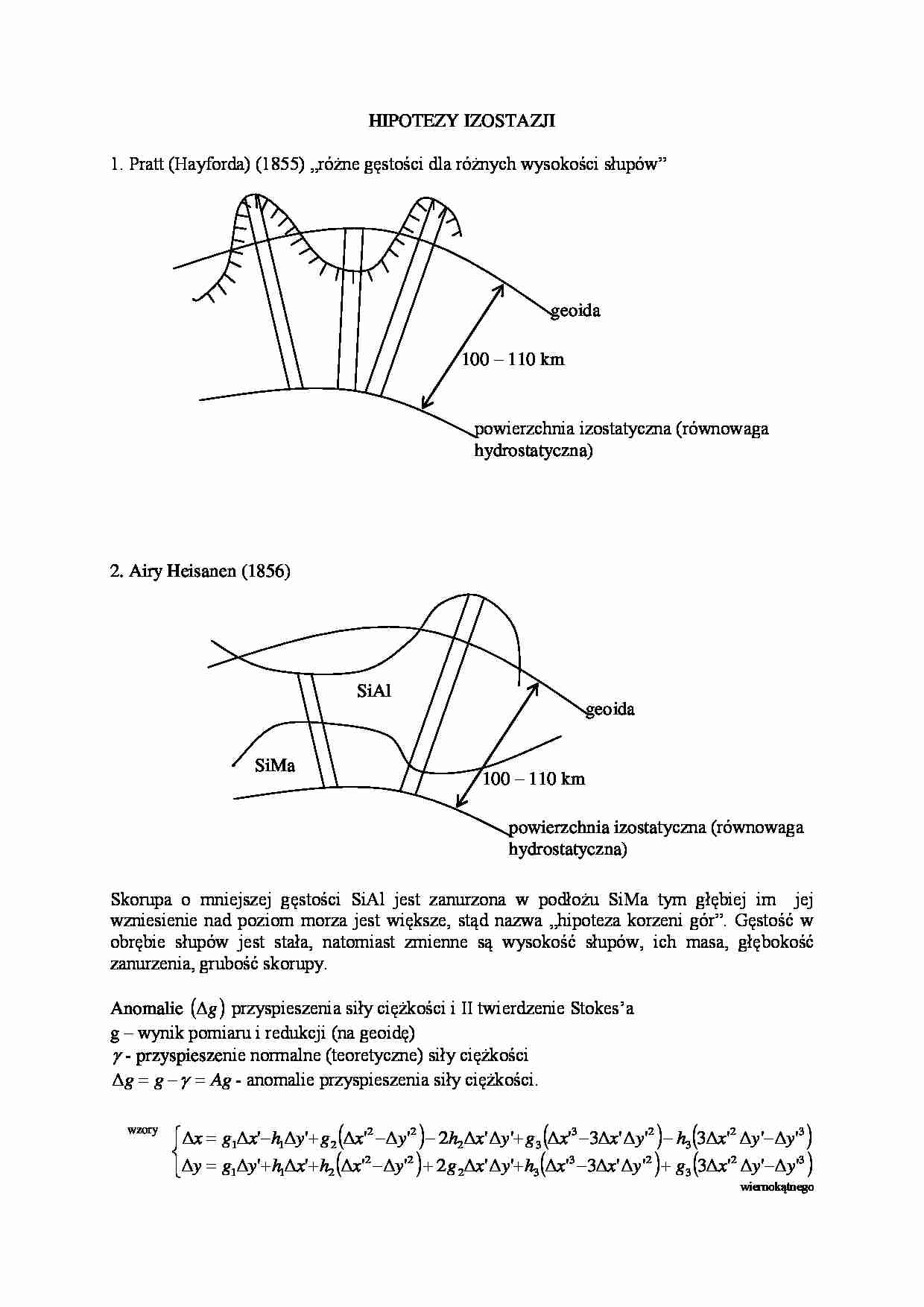
1. Pratt (Hayforda) (1855) „różne gęstości dla różnych wysokości słupów”
geoida
100 – 110 km
powierzchnia izostatyczna (równowaga
hydrostatyczna)
2. Airy Heisanen (1856)
SiAl
geoida
SiMa
100 – 110 km
powierzchnia izostatyczna (równowaga
hydrostatyczna)
Skorupa o mniejszej gęstości SiAl jest zanurzona w podłożu SiMa tym głębiej im jej
wzniesienie nad poziom morza jest większe, stąd nazwa „hipoteza korzeni gór”. Gęstość w
obrębie słupów jest stała, natomiast zmienne są wysokość słupów, ich masa, głębokość
zanurzenia, grubość skorupy.
Anomalie g  przyspieszenia siły ciężkości i II twierdzenie Stokes’a
g – wynik pomiaru i redukcji (na geoidę)
 - przyspieszenie normalne (teoretyczne) siły ciężkości
g  g    Ag - anomalie przyspieszenia siły ciężkości.
wzory










x  g1x'h1y ' g 2 x'2 y '2  2h2 x' y ' g3 x'3 3x' y '2  h3 3x'2 y 'y '3

2
2
3
2
2
3
y  g1y ' h1x' h2 x' y '  2 g 2 x' y ' h3 x' 3x' y '  g 3 3x' y 'y'


wiernokątnego
odwzorowania
płaskiego
transformacja Helmerta ( dla małych obszarów) – wystarczą 2 punkty wspólne - 4
niewiadome (go, ho, g1, h1)
Współrzędne bieguna: x'0 
 x'
y '0 
 y' .
n
n
x, y – duże to transformacja Helmerta jest za mało dokładna, dlatego na większych
obszarach trzeba mieć więcej niż dwa punkty dostosowania.
4. Transformacja z pasa na pas w odwzorowaniu Gaussa - Krgera.
g1  cos 2 0
0’ 0
h1  sin 2 0
g2  

3 p2
2
 2  cos 2 B0  t0 1  0
N0 
2
t0  tgB0 0  e'2 cos 2 B0
h2=... g3, h3 – odpowiednie
wzory
x', y'  x, y 

y0’
y0
P0 (x0’, y0’)
x0’
x ' 0  x0 y ' 0   y 0  ' 0   0
x0, y0 można obliczyć dla danej elipsy.
Tablice Tarczy – Hornocha i Hristowa – są w nich przeliczenia między pasami. Wszystkie
tablice zabezpieczają dokładności centymetrowe.
x0
5. Transformacja współrzędnych geodezyjnych (B, L) z jednej elipsy na drugą.
Elipsoida E’
Elipsoida E
B'1 , L'1 
B1 , L1 

B ' n , L ' n 

Bn , Ln 
x'1  N '1 cos B'1 cos L'1
x1  N1 cos B1 cos L1
y '1  N '1 cos B'1 sin L'1
y1  N1 cos B1 sin L1
z '1  N '1 1  e 2  sin B'1 z1  N1  1  e 2  sin B1
„e“ jest inne niż przy z’1.
 x   x'0   x'
m x 
     
 
 y    y '0    y '  C  m y 
 z   z'   z'
m 
   0  
 z
przesunięcie
współczynniki kierunkowe
skale
Transformacja między odwzorowaniami:
xs , ys   B, L   X GK , YGK 
odwz. Soldnera  wsp. geodezyjne  odwz. Gaussa  Krugera
... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz