Linia geodezyjna- opracowanie

Nasza ocena:

5
Pobrań: 770
Wyświetleń: 3542
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
Linia geodezyjna- opracowanie - strona 1 Linia geodezyjna- opracowanie - strona 2 Linia geodezyjna- opracowanie - strona 3

Fragment notatki:

LINIA GEODEZYJNA (ORTODROMA)
Taka krzywa na powierzchni, która:
- jest najkrótszą odległością między dwoma punktami na powierzchni
- gdyby na punkt poruszający się po powierzchni nie działała żadna siła, biegłby on po
tej krzywej
- w każdym jej punkcie normalna główna do krzywej jest zarazem normalną do
powierzchni w tym punkcie
- płaszczyzna ściśle styczna do krzywej w każdym jej punkcie zawiera normalną do
powierzchni w tym punkcie
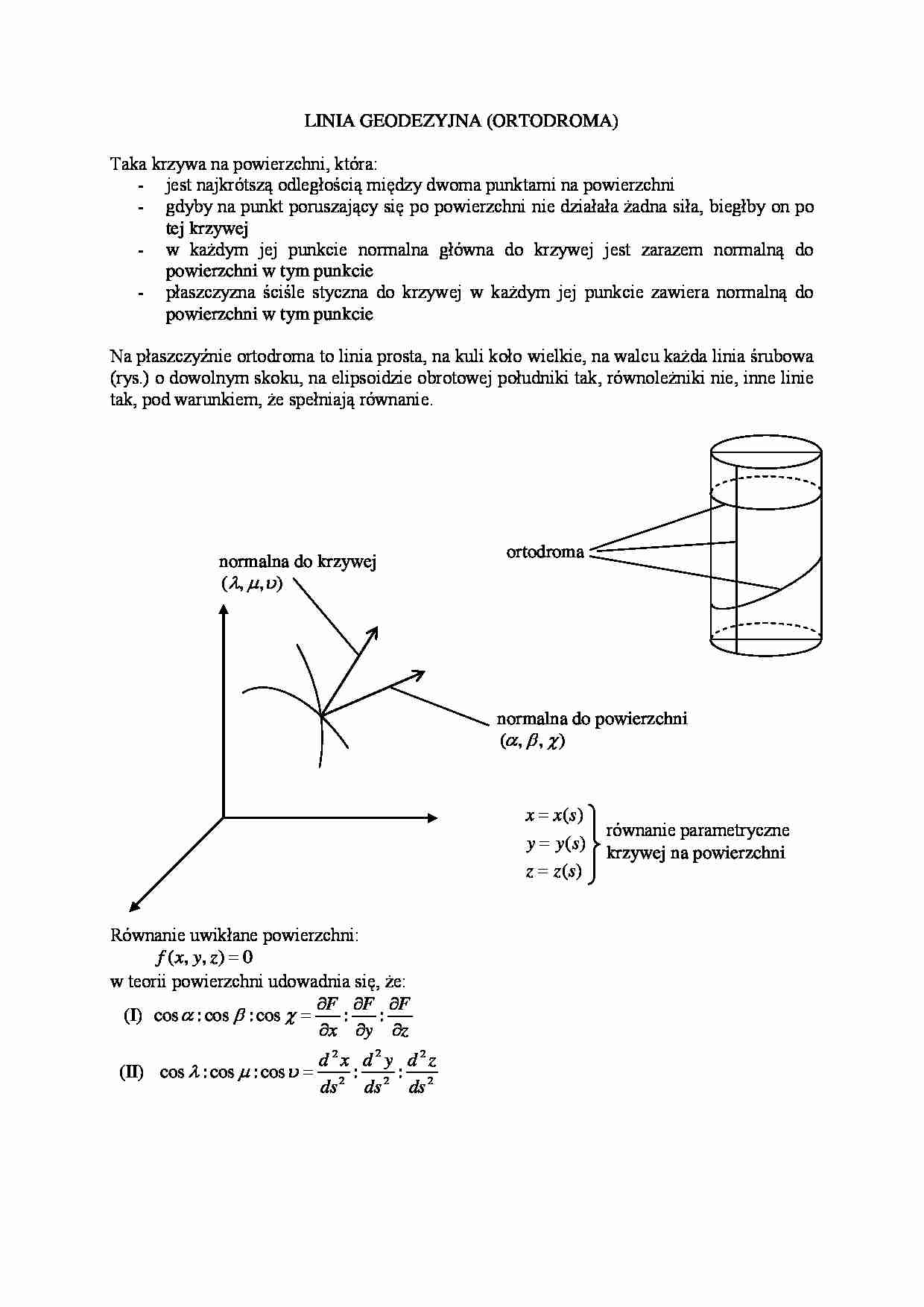
Na płaszczyźnie ortodroma to linia prosta, na kuli koło wielkie, na walcu każda linia śrubowa
(rys.) o dowolnym skoku, na elipsoidzie obrotowej południki tak, równoleżniki nie, inne linie
tak, pod warunkiem, że spełniają równanie.
normalna do krzywej
( ,  , )
ortodroma
normalna do powierzchni
( ,  ,  )
x  x( s)
y  y ( s)
z  z ( s)
Równanie uwikłane powierzchni:
f ( x, y, z )  0
w teorii powierzchni udowadnia się, że:
F F F
:
:
(I) cos  : cos  : cos  
x y z
(II) cos  : cos  : cos  
d 2x d 2 y d 2z
:
:
ds 2 ds 2 ds 2
równanie parametryczne
krzywej na powierzchni
Dla elipsoidy obrotowej:
x2  y2 z 2
 2 1  0
a2
b
2
2
2
b ( x  y )  a 2 z 2  a 2b 2  0
 a2

F ( x, y , z )  x 2  y 2   2 z 2  a 2   0
b



liczymy pochodne cząstkowe:
F
 2x
x
F
 2y
y
F
a2
2 2 z
z
b
Proporcja z równań (I) i (II):
d 2x
d2y
: 2x  2 : 2 y
ds 2
ds
2
d y
d 2x
x 2 y 2
ds
ds
2
d y
d 2x
x 2 y 2 0
ds
ds
Całkujemy
dy
dx
x
y
C
ds
ds
xdy  ydx  Cds
ds rzutujemy na
otrzymujemy d
x  R cos L
Kawałek krzywej ds
płaszczyznę XY i
r
y  R sin L
r 2  x2  y2
Element pola:
1
dP  rd
2
d  rdL
1
dP  r 2 dL
2
dL
L
d
y
 tgL
x
y
x
 y
d 
x
dL    2
 y
1  
x
xdy  ydx
dL  2
x  y2
1
1
xdy  ydx 1
dP  r 2 dL  ( x 2  y 2 ) 2
 ( xdy  ydx )
2
2
x  y2
2
L  arctg
r 2 dL  xdy  ydx  Cds
dL
r2
C
ds
ds cos A  MdB
ds sin A  N cos BdL
dL
sin A
sin A


ds N cos B
r
dL
sin A
r2
 C  r2
 r sin A
ds
r
r sin A  const
równanie Clairaut
B  dB
ds
MdB
A
B
N cos BdL
L
L  dL
Iloczyn promienia równoleżnika i sinusa azymutu linii geodezyjnej jest stały na całej jej
długości.
N cos B sin A  const
u - szerokość zredukowana
a - duża półoś elipsoidy
inna postać równania
a cos u sin A  const
KSZTAŁT LINII GEODEZYJNEJ NA POWIERZCHNI ELIPSOIDY OBROTOWEJ
A  90
A  0 - południki
A  90 - równik
linie
geodezyjne
równik
równoleżniki nie spełniają 1., 3. i
4. definicji...
A  30
A  30
150
PRZEBIEG LINII GEODEZYJNEJ WZGLĘDEM WZAJEMNYCH PRZEKROJÓW
NORMALNYCH
A21
Dowodzi się, że
a bs
1
A12   1  ( 1   1 ' )
3
1
A21   2  ( 1   1 ' )
3
4

S
a  s  1  4 sin 2 A1 cos 2 A1
90 N 1
P2
b
1
1 '
2
3
A12
a
P
1
2
3
s
1
3
1
2
1
3
... zobacz całą notatkę



Komentarze użytkowników (1)

Zaloguj się, aby dodać komentarz

ryszard napisał(a):

2017-03-13 18:26:42

Zbyt mało rysunków i brak linii geodezyjnych elipsoidy nieobrotowej.