To tylko jedna z 9 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


WYKŁAD 5
KONSTRUKCJA CAŁKI WZGLĘDEM MIARY
(Ω, U, μ) - przestrzeń z miarą
ƒ: Ω→R
I ETAP KONSTRUKCJI CAŁKI WZGLĘDEM MIARY
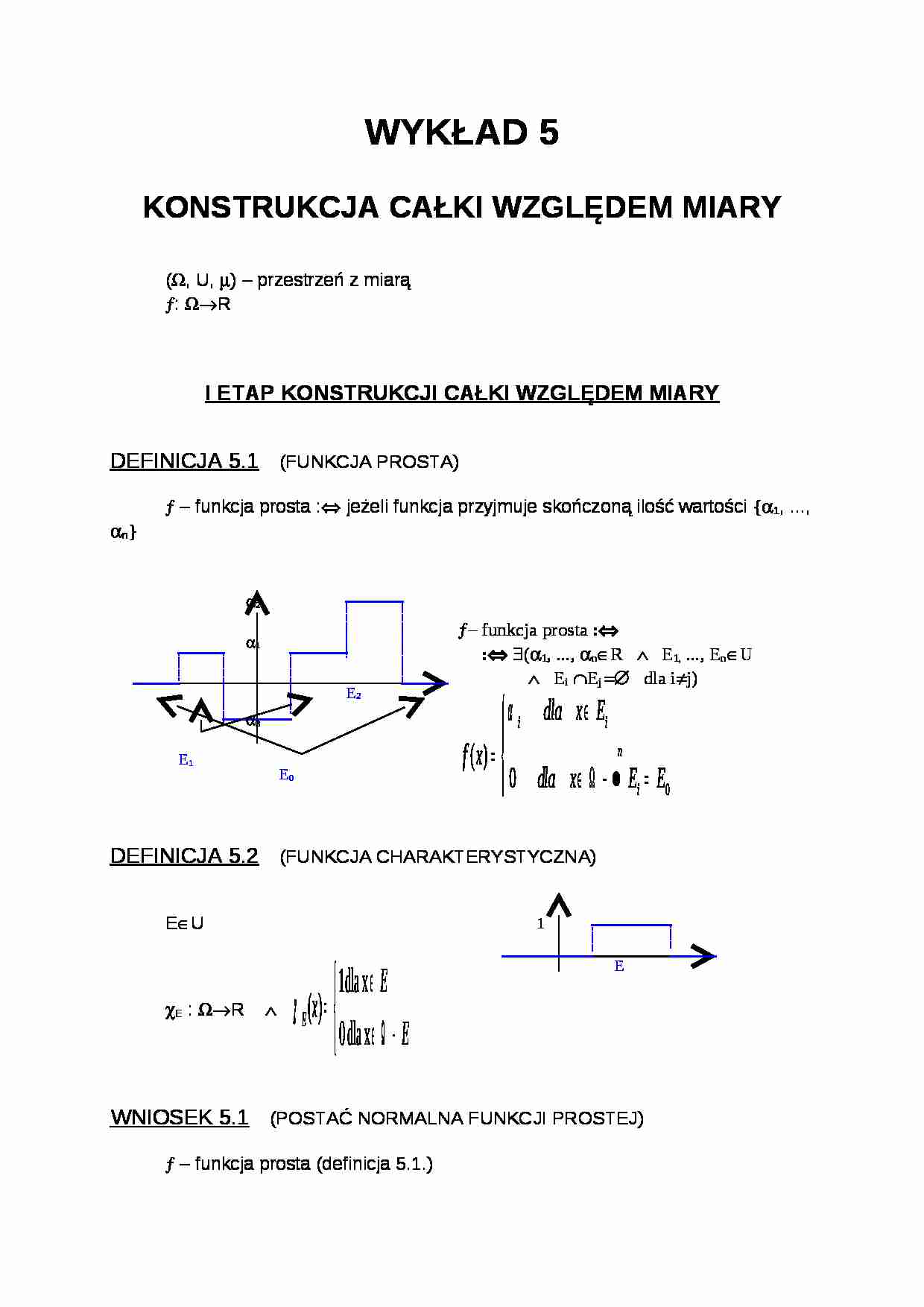
DEFINICJA 5.1 (FUNKCJA PROSTA)
ƒ - funkcja prosta :⇔ jeżeli funkcja przyjmuje skończoną ilość wartości {α1, ..., αn}
DEFINICJA 5.2 (FUNKCJA CHARAKTERYSTYCZNA)
E∈U χE : Ω→R ∧ WNIOSEK 5.1 (POSTAĆ NORMALNA FUNKCJI PROSTEJ)
ƒ - funkcja prosta (definicja 5.1.)
Objaśnienie:
Gdy: x∈Ek , to: L=ƒ(x)= αk ⇒ L=P
Każda funkcja prosta jest kombinacją liniową funkcji charakterystycznych.
Istnieje nieskończenie wiele postaci normalnych funkcji prostej.
TWIERDZENIE 5.1 (WŁASNOŚCI FUNKCJI PROSTYCH)
ε - zbiór wszystkich funkcji prostych określonych na Ω
∀ƒ,g∈ε ∀α,β∈R (αƒ+βg)∈ ε
∀ƒ,g∈ε sup.{ƒ,g }∈ ∧ inf{ƒ,g}∈ ε
∀ x∈Ω (sup.{ƒ,g })(x)=max{ƒ(x),g(x)}
∀ x∈Ω (inf.{ƒ,g })(x)=min{ƒ(x),g(x)}
∀ƒ∈ε ƒ∈ ε
∀ƒ∈ε ∀E∈U ƒχE∈ ε
∀ƒ,g∈ε (ƒg)∈ ε
Dowód:
Ad. 1) Niech: x={ Ei∩Fj: i={0, ..., n}∧ j={0, ..., m}}
Uwaga:
A∩B=∅ to χA∪B = χA+χB gdzie Ei∩Fj są parami rozłączne,
tzn. (Ei∩Fj)∩( Ei∩Fk)=∅ dla Ad. 2.) korzystając z ad. 1) można zapisać:
analogicznie:
Ad. 3.) Ad. 4.)
DEFINICJA 5.3 (FUNKCJA PROSTA CAŁKOWALNA)
(…)
… CAŁKI WZGLĘDEM MIARY
DEFINICJA 5.6 (FUNKCJA CAŁKOWALNA)
Niech:
ƒ: Ω→R
ƒ+: Ω ∋ →ƒ+(x) := max {ƒ (x), 0}
ƒ-: Ω∋ →ƒ_(x) := max {-ƒ (x), 0}
ƒ = ƒ+ - ƒ- ƒ - μ- całkowalna :⇔ ƒ+, ƒ- są μ- całkowalne
tzn. ∃ ((un)⊂ε+, un ∧ (vn)⊂ε+, vn )
∧ := Uwaga:
L1(μ) - zbiór funkcji μ- całkowalnych
ε+ ⊂ ε1+ ⊂ L1(μ)
KONSTRUKCJA CAŁKI WZGLĘDEM MIARY - PODSUMOWANIE - Całka z funkcji prostej
to Całka z funkcji nieujemnej
, un…
... zobacz całą notatkę






Komentarze użytkowników (0)