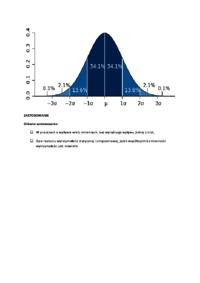
Niezawodność systemów - rozkład normalny - omówienie
- Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie
- Niezawodność systemów
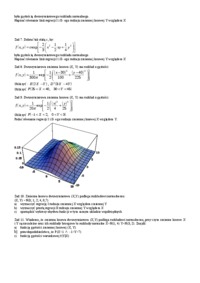
, z których żadna z nich nie może być uznana za dominującą. Funkcja gęstości prawdopodobieństwa wyraża się wzorem: Zbiór wartości funkcji: σ2...