To tylko jedna z 23 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


8. Metody energetyczne
8. METODY ENERGETYCZNE
Metody energetyczne – metody analizy odkształceń konstrukcji prętowych na podstawie
energii potencjalnej zgromadzonej w obcią onej konstrukcji
8.1. Energia sprę ysta w konstrukcji prętowej
Energia potencjalna (sprę ysta, odkształcenia) równa jest pracy sił zewnętrznych
obcią ających konstrukcję.
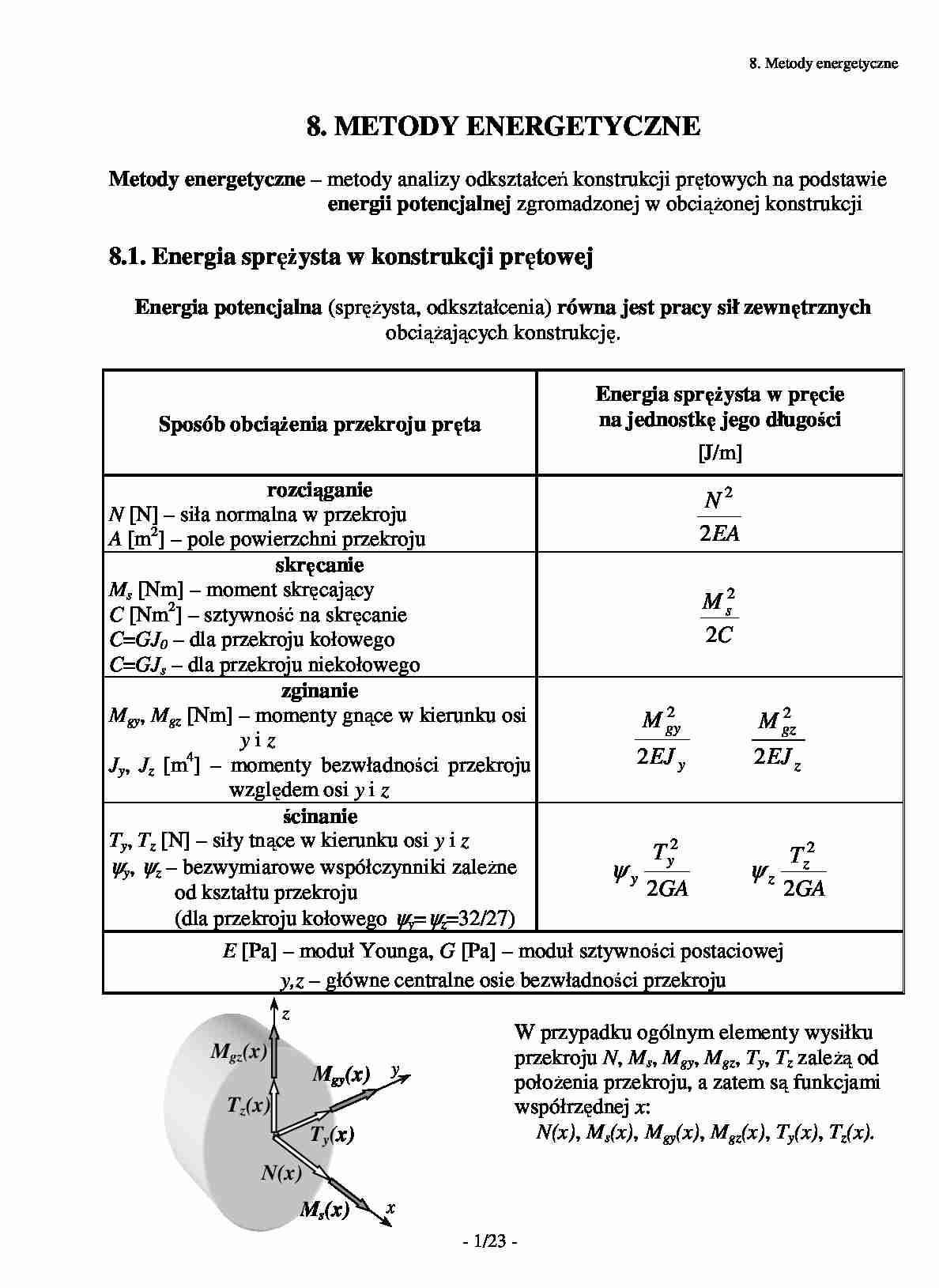
Energia sprę ysta w pręcie
na jednostkę jego długości
Sposób obcią enia przekroju pręta
[J/m]
rozciąganie
N2
N [N] – siła normalna w przekroju
2 EA
A [m2] – pole powierzchni przekroju
skręcanie
Ms [Nm] – moment skręcający
M s2
2
C [Nm ] – sztywność na skręcanie
2C
C=GJ0 – dla przekroju kołowego
C=GJs – dla przekroju niekołowego
zginanie
2
2
Mgy, Mgz [Nm] – momenty gnące w kierunku osi
M gy
M gz
yiz
4
2 EJ y
2 EJ z
Jy, Jz [m ] – momenty bezwładności przekroju
względem osi y i z
ścinanie
Ty, Tz [N] – siły tnące w kierunku osi y i z
Ty2
Tz2
ψy, ψz – bezwymiarowe współczynniki zale ne
ψy
ψz
2GA
2GA
od kształtu przekroju
(dla przekroju kołowego ψy=ψz=32/27)
E [Pa] – moduł Younga, G [Pa] – moduł sztywności postaciowej
y,z – główne centralne osie bezwładności przekroju
z
Mgz(x)
Mgy(x) y
Tz(x)
Ty(x)
W przypadku ogólnym elementy wysiłku
przekroju N, Ms, Mgy, Mgz, Ty, Tz zale ą od
poło enia przekroju, a zatem są funkcjami
współrzędnej x:
N(x), Ms(x), Mgy(x), Mgz(x), Ty(x), Tz(x).
N(x)
Ms(x)
x
- 1/23 -
8. Metody energetyczne
Energia zgromadzona w konstrukcji prętowej
l
l M 2
l M 2
l
l
Ty 2
M s2
Tz 2
N2
gy
gz
U =∫
dx + ∫
dx + ∫
dx + ∫
dx + ∫ψ y
dx + ∫ψ z
dx
2 EA
2 EA
0 2 EA
0 2C
0 2 EJ y
0 2 EJ z
0
0
l
x – współrzędna określająca poło enie przekroju,
l – długość całej konstrukcji prętowej
do pominięcia
w przypadku konstrukcji zbudowanej
z prętów smukłych
l
l M2
l M2
N2
M s2
gy
U =∫
dx + ∫
dx + ∫
dx + ∫ gz dx
0 2 EA
0 2C
0 2 EJ y
0 2 EJ z
l
na ogół do pominięcia
w konstrukcjach
zginanych i skręcanych
8.2. Siły uogólnione, współrzędne uogólnione, układ Clapeyrona
(Benoit Paul Emil Clapeyron 1799-1864)
siła uogólniona
dowolne obcią enie działające na ciało
P
współrzędna uogólniona
przemieszczenie odpowiadające sile
uogólnionej
f
siła skupiona P
przemieszczenie f
punktu przyło enia siły
na kierunku linii działania siły
A
A1
moment skręcający Ms
kąt skręcenia wywołany działaniem
momentu skręcającego Ms
moment gnący Mg
kąt ugięcia wywołany działaniem
momentu gnącego Mg
pole zakreskowane na rysunku
obcią enie ciągłe q
- 2/23 -
8. Metody energetyczne
Układ Clapeyrona to układ mechaniczny, w którym:
1. materiał jest idealnie sprę ysty,
2. w adnym punkcie naprę enia nie przekraczają granicy proporcjonalności,
3. mo na stosować zasadę superpozycji (działanie jednych sił uogólnionych nie
zmienia charakteru działania innych sił)
Jeśli siły uogólnione działające na układ przykładane są jednocześnie, wzrastają
równomiernie i osiągają swoje końcowe wartości w tej samej chwili
to
energia sprę ysta układu równa jest pracy sił uogólnionych
1
1
1
1
1 n
U = P f1 + P2 f 2 + ... + Pi f i + ... + Pn f n = ∑ Pi f
(…)
… – przykład ustroju statycznie niewyznaczalnego
y
P
C
A
f
RA
RC
Nale y wyznaczyć 3 niewiadome reakcje: RA, RB, RC.
Do dyspozycji mamy 2 równania równowagi: ∑ F y = 0
B
x
RB
∑MK = 0
∑MJ = 0
albo ∑ M K = 0
(K, J – dowolnie wybrane punkty płaszczyzny)
Trzecie równanie wyra ające równowagę sił w kierunku osi x: ∑ Fx = 0 jest spełnione.
Liczba niewiadomych przewy sza o 1 liczbę równań równowagi. Układ jest zatem…
…
Stan "0"
l
fD = ∫
B
stan "1"
M g mg
0
1
=
EJ
EJ
a
dx = ∫
0
M g mg
EJ
b
dx + ∫
0
M g mg
EJ
dx =
1 a a 2 Pb 1 a a Pb 1 Pb
Pba 2
2 2 4 ⋅ 3 2 + 2 2 4 ⋅ 2 + 3 2 + 0 = 16 EJ
- 16/23 -
8. Metody energetyczne
8.8. Równania Maxwella-Mohra (równania kanoniczne metody sił)
y
P2
P1
Pk
B
A
RA
(
M g0)
M
X1
Xi
Xn
P2
P1
x
RB
Stan „0”
Pk
B
A
Układ Clapeyrona
belka na n+2 podporach
(układ n-krotnie…
... zobacz całą notatkę






Komentarze użytkowników (0)