Adresy internetowe, pod którymi można znaleźć wykłady z Wytrzymałości Materiałów:
Politechnika Krakowska
http://limba.wil.pk.edu.pl/kwm-edu.html
Politechnika Łódzka
http://kmm.p.lodz.pl/dydaktyka
________________________________________________
Wykład 5. Skręcanie nieskrępowane prętów o przekroju prostokątnym.
Hipoteza kinematyczna przyjęta jak poprzednio, rozważamy teorię skręcania prętów
przedstawioną w wykładzie nr 2 i kolejnych. Rozwiążmy zadanie skręcania pręta o dowolnym
przekroju znajdując funkcję Prandtla bezpośrednio, metodą numeryczną. Spełnia ona, jak
wiadomo, niejednorodne równanie harmoniczne w obszarze S:
(1)
ϕ ,11 + ϕ ,22 = −2GΘ '
i jest równa zeru na brzegu obszaru S.
Rozpatrzmy przekrój prostokątny (oczywiście, analityczne wyrażenie dla funkcji Prandtla jest
możliwe, jednak w miarę komplikowania sie kształtu konturu jego postać jest coraz bardziej
skomplikowana i podejście analityczne wymaga złożonych przekształceń symbolicznych,
podczas gdy algorytm rozwiązania numerycznego jest zawsze taki sam, powtarzalny)
Prostokąt o bokach a i b pokryjemy siatką punktów, w których obliczymy wartości funkcji
Prandtla. Na boku a umieścimy M punktów odległych od siebie o dx, na boku b umieścimy N
punktów odległych o dy. Przyjmiemy, że GΘ=1.
Uprościmy zapis następująco:
i
ϕ (x1 , x 2j ) = ϕ ij
(2)
ponieważ wszystkie wartości funkcji Prandtla w punktach x1i, x2j utworzą wektor
niewiadomych, potrzebna jest jeszcze inna numeracja: numerując niewiadome rzędami
otrzymamy dla danego i, j niewiadomą nr k, oznaczoną f(k), według wzoru:
f ( k ) = ϕ ij gdzie k=(i-1)M+j
(3)
Jak wiadomo, drugą pochodną ze względu na x1 (i podobnie dla x2) można w przybliżeniu
zapisać następująco:
∂ 2ϕ
∂x1
(x1i ,x2j ) = ϕ
2
i +1, j
− 2ϕ ij + ϕ i −1, j
dx1
2
∂ 2ϕ
∂x 2
(x1i ,x2j ) = ϕ
2
i , j +1
− 2ϕ ij + ϕ i , j −1
dx 2
(4)
2
Równanie różniczkowe (1) można więc zastąpić układem równań z niewiadomymi f(k),
zastępując pochodne ich przybliżonymi wartościami różnicowymi, dla każdego punktu w
obszarze S. (Na brzegu ∂S wartości f są dane i równe zeru).
Przyjmijmy, że GΘ =1. Nie zmniejsza to ogólności rozważań, zawsze możemy wynik
pomnożyć przez właściwe GΘ. Dla punktu o współrzędnej i,j otrzymamy równanie (5):
1
ϕ i +1, j − 2ϕ ij + ϕ i −1, j ϕ i , j +1 − 2ϕ ij + ϕ i , j −1
+
= −2
dx1 2
dx 2 2
1
dx1
ϕ i +1, j +
2
1
1
1
1
ϕ i −1, j − 2 2 + 2 ϕ ij +
ϕ i , j +1 +
ϕ i , j −1 = −2
2
2
2
dx
dx1
dx 2
dx 2
1 dx1
1
(4)
(5)
Mamy tyle równań ile niewiadomych (punkty wewnętrzne w S). Schemat budowy układu
równań na siatce punktów przedstawia rysunek 1. Pokazano tu schemat równania napisanego
dla niewiadomej o numerze 55 czyli dla i=6 i j=5.
b
a
1 2
11dy 12
21 22
31 32
41 42
51 52
61 62
71 72
81 82
91 92
dx
3
13
23
33
43
53
63
73
83
93
4
14
24
34
44
54
64
74
84
94
5
15
25
35
45
55
65
75
85
95
6
16
26
36
46
56
66
76
86
96
7
17
27
37
47
57
67
77
87
97
8
18
28
38
48
58
68
78
88
98
9 10
19 20
29 30
39 40
49 50
59 60
69
(…)
… prostokątnych wymaga
rozwiązania równania różniczkowego o pochodnych cząstkowych, co może być czasochłonne
- większość tablic inżynierskich oraz podręczniki do Wytrzymałości Materiałów (w tym
podręcznik A. Jakubowicza i Z. Orłosia) publikują tabele do wymiarowania takich
przekrojów. Tabele takie zawierają współczynniki do obliczania sztywności skrętnej,
wskaźnika wytrzymałości na skręcanie oraz maksymalnego…
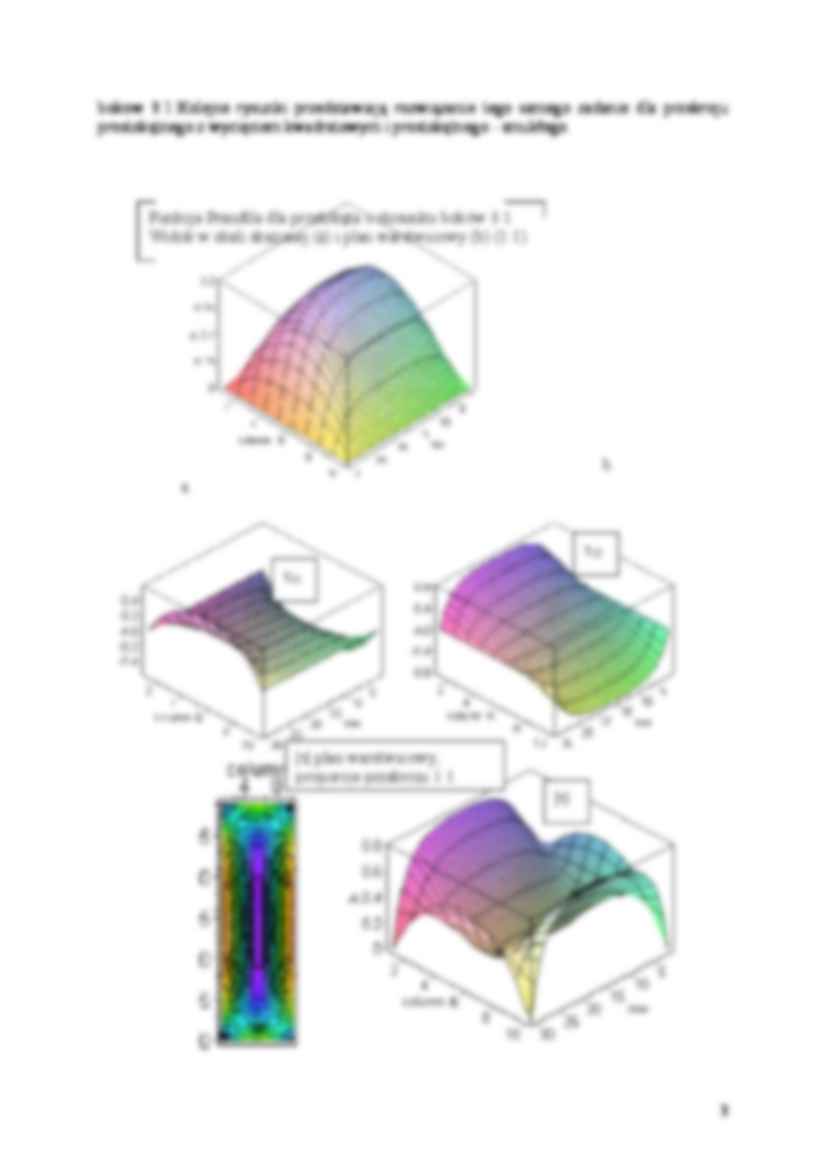
….Kolejne rysunki przedstawiają rozwiązanie tego samego zadanie dla przekroju
prostokątnego z wycięciem kwadratowym i prostokątnego - smukłego.
Funkcja Prandtla dla prostokąta o stosunku boków 3:1.
Widok w skali skażonej (a) i plan warstwicowy (b) (1:1)
b.
a.
τ32
τ31
|τ| plan warstwicowy,
proporcje przekroju 1:1
|τ|
3
Funkcja Prandtla dla przekroju z wycięciem - (a) widok i (b) plan warstwicowy. Wykres c…
... zobacz całą notatkę





Komentarze użytkowników (0)