To tylko jedna z 10 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


WEKTORY
Wektorami nazywamy wielkoÑci, które charakteryzuj si
wartoÑci liczbow, kierunkiem i zwrotem, a ponadto moóna je
sk»ada (dodawa) zgodnie z regu» równoleg»oboku.
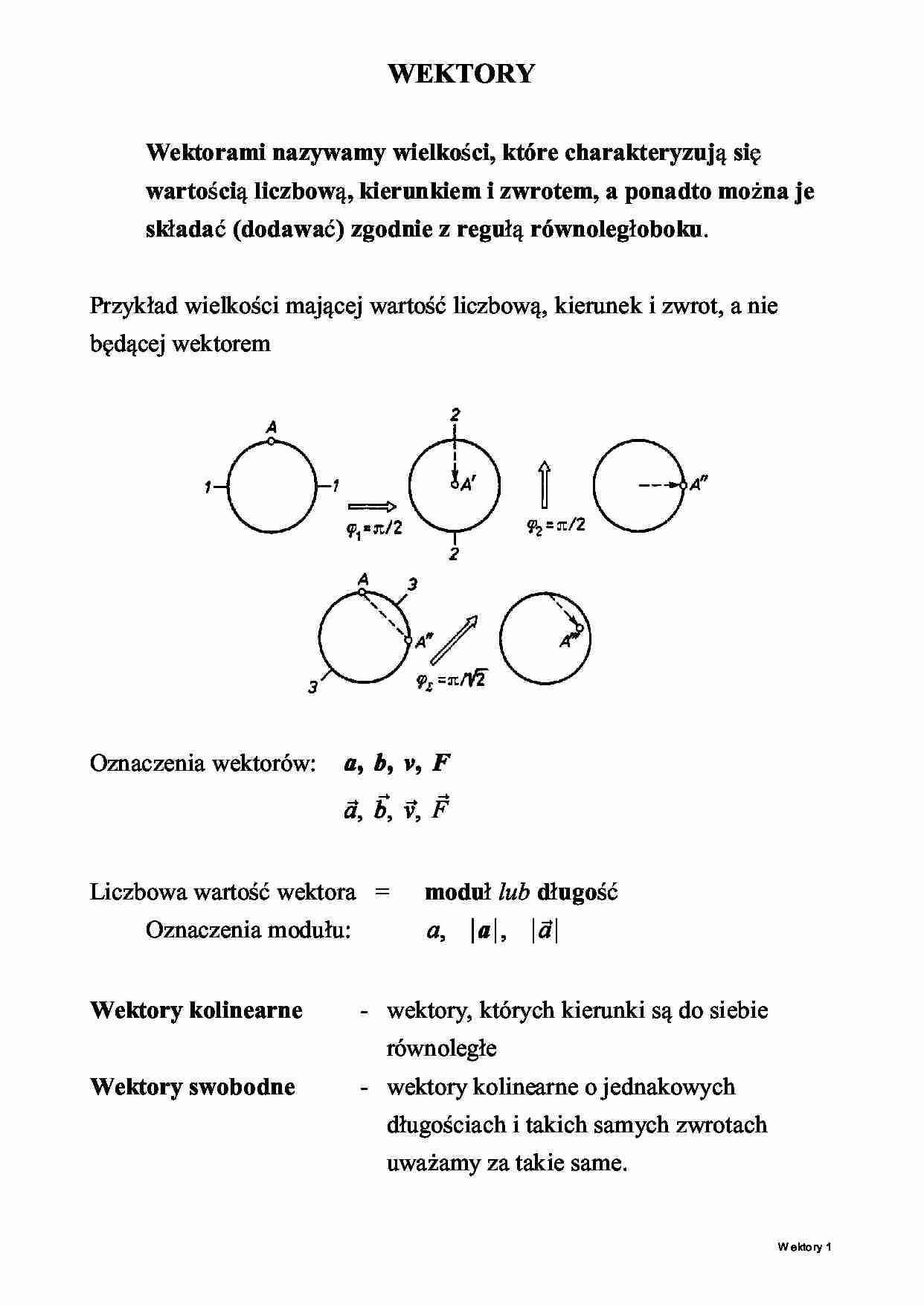
Przyk»ad wielkoÑci majcej wartoÑ liczbow, kierunek i zwrot, a nie
bdcej wektorem
Oznaczenia wektorów:
Liczbowa wartoÑ wektora =
modu» lub d»ugoÑ
Oznaczenia modu»u:
Wektory kolinearne
- wektory, których kierunki s do siebie
równoleg»e
Wektory swobodne
- wektory kolinearne o jednakowych
d»ugoÑciach i takich samych zwrotach
uwaóamy za takie same.
W ektory 1
Dodawanie (sk»adanie) i odejmowanie wektorów
a) suma -
metoda równoleg»oboku lub metoda wieloboku
Na ogó»:
b) róónica -
róónic wektorów
dodany do wektora
i
jest taki wektor , który
daje wektor
Na ogó»:
Mnoóenie wektora przez skalar:
,
kierunki wektorów
zwrot:
i
zgodny ze zwrotem
gdy
przeciwny zwrotowi
s zgodne
gdy
W ektory 2
Wersor
kaódy wektor moóna przedstawi w postaci
- wektor jednostkowy, wersor wektora
Wersor jest wielkoÑci bezwymiarow:
Rzut wektora na oÑ
Rzut wektora na oÑ moóe by dodatni, ujemny lub równy zeru
Wyraóenie wektora przez jego rzuty na osie uk»adu wspó»rzdnych
Wektor
i
moóna przedstawi w postaci liniowej kombinacji wersorów
:
lub ogólnie:
- sk»adowe wektora
W ektory 3
Wektor po»oóenia
W ektory 4
ILOCZYN SKALARNY WEKTORÓW
jeÑli
, to
Iloczyn skalarny jest:
przemienny:
rozdzielny wzgldem dodawania:
Iloczyn skalarny wersorów osi kartezja½skiego uk»adu odniesienia
,
- symbol Kroneckera,
ZaleónoÑ iloczynu skalarnego od sk»adowych
Kombinacja typu
nie zaleóy od wyboru osi, jest
niezmiennikiem (inwariantem)
Ponadto moóna pokaza, óe
W ektory 5
ILOCZYN WEKTOROWY WEKTORÓW
Iloczynem wektorowym wektorów
jest wektor
dany wzorem
wersor normalny do p»aszczyzny, w której leó wektory
i tworzcy z tymi wektorami uk»ad prawoskrtny
Dwa sposoby zapisu iloczynu wektorowego
Wyraóenie
jest liczbowo równe polu powierzchni
równoleg»oboku rozpitego na wektorach
Wektory
typu
nazywane s pseudowektorami. PrzejÑcie od
prawoskrtnego uk»adu wspó»rzdnych do lewoskrtnego uk»adu
wspó»rzdnych powoduje zmian zwrotu pseudowektorów na przciwne,
natomiast nie zmienia zwrotów wektorów w Ñcis»ym sensie.
Iloczyn wektorowy nie jest przemienny
Iloczyn wektorowy jest rozdzielny wzgldem dodawania
W ektory 6
Iloczyny wektorowe wersorów osi uk»adu wspó»rzdnych
Zapis iloczynu wektorowego w postaci wyznacznika
Iloczyn mieszany (skalarno-wektorowy) wektorów
Wyraóenie
jest równe liczbowo objtoÑci równoleg»oboku
rozpitego na wektorach
Zachodzi wic
W ektory 7
Podwójny iloczyn wektorowy
Wektor
jest prostopad»y do iloczynu
, a wic jest liniow
kombinacj wektorów
Moóna pokaza, óe
Pochodna wektora
Rozwaómy wektor
- sta»e w czasie wersory osi uk»adu wspó»rzdnych
- znane funkcje czasu
Analizujc granic odpowiedniego ilorazu róónicowego otrzymujemy
W fizyce czsto stosuje si kropk nad liter symbolizujc wielkoÑ dla
oznaczenia pochodnej tej wielkoÑci po czasie
Moóna wic zapisa
Dla wektora po»oóenia
poruszajcego si punktu materialnego
W ektory 8
Róóniczka funkcji wektorowej
W szczególnoÑci
Przyrost funkcji wektorowej w cigu ma»ego, ale sko½czonego odstpu
czsu
Pochodne i róóniczki iloczynów funkcji wektorowych
a) iloczyn funkcji skalarnej i funkcji wektorowej
b) iloczyn dwóch funkcji wektorowych
W ektory 9
Pochodna wersora
- prdkoÑ ktowa obracania si wektora
Wektor
leóy w p»aszczyïnie, w której w danej chwili obraca si
wektor
i zwrócony jest w t sam stron, w któr zachodzi obrót.
W ektory 10
... zobacz całą notatkę






Komentarze użytkowników (0)