To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
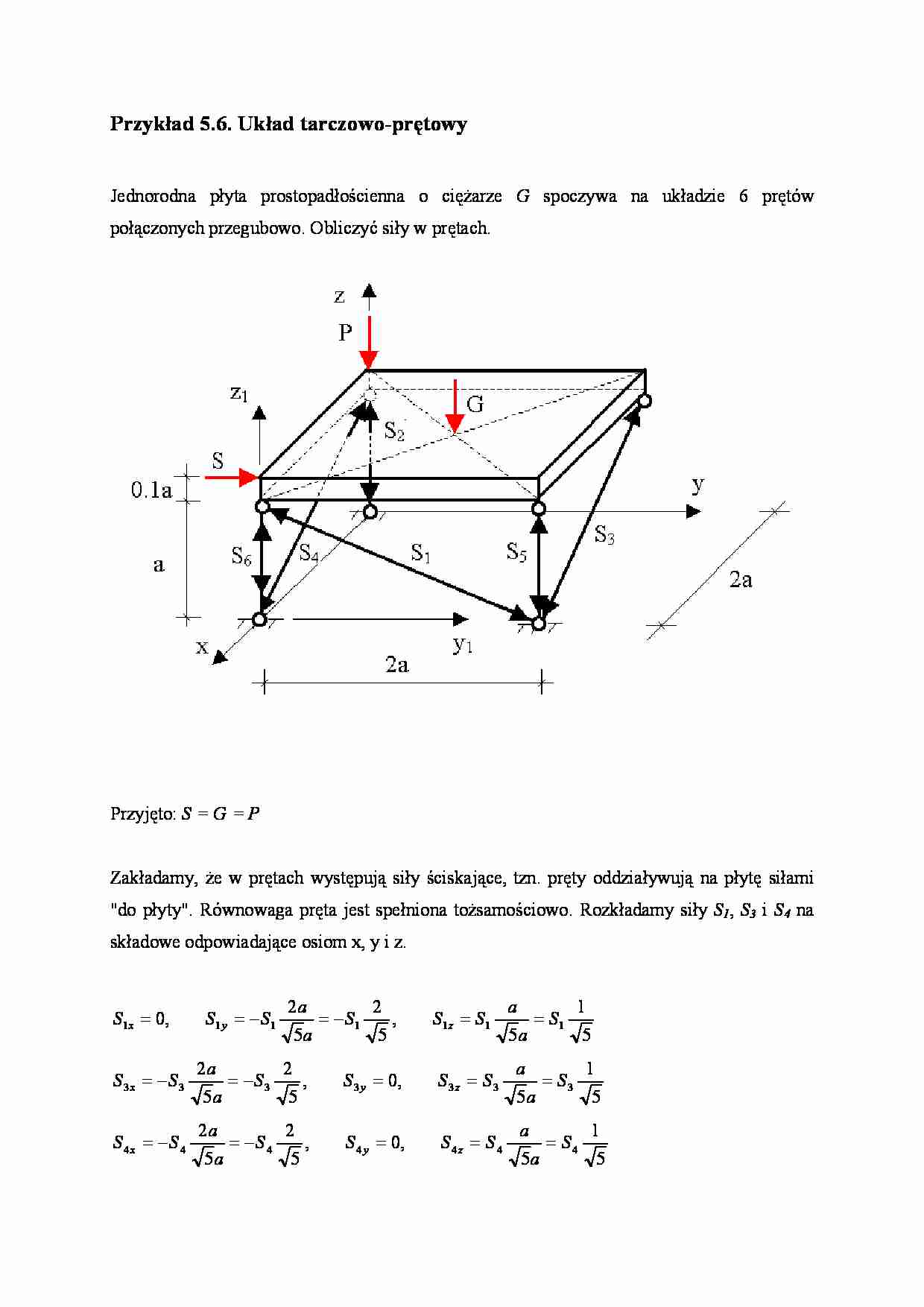

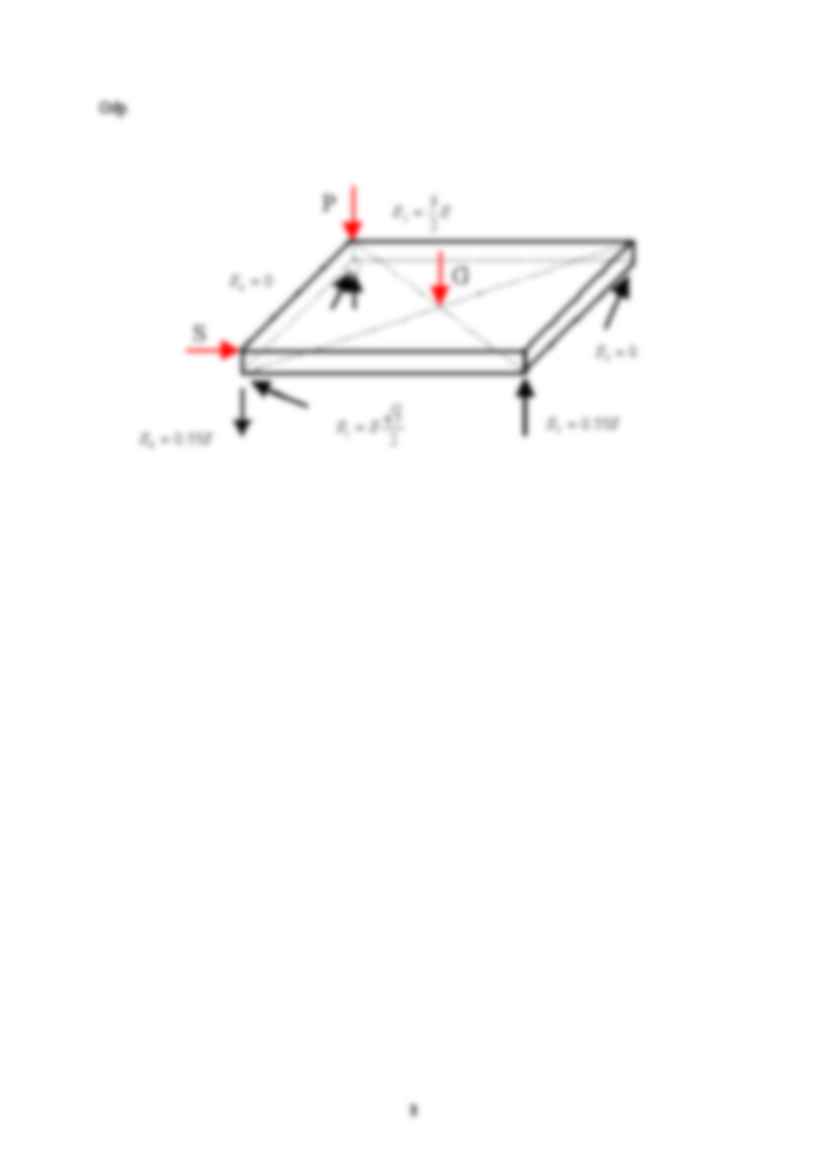
Przykład 5.6. Układ tarczowo-prętowy Jednorodna płyta prostopadłościenna o ciężarze G spoczywa na układzie 6 prętów połączonych przegubowo. Obliczyć siły w prętach. Przyjęto: S = G = P Zakładamy, że w prętach występują siły ściskające, tzn. pręty oddziaływują na płytę siłami "do płyty". Równowaga pręta jest spełniona tożsamościowo. Rozkładamy siły S1 , S3 i S4 na składowe odpowiadające osiom x, y i z. 5 1 5 , 5 2 5 2 , 0 1 1 1 1 1 1 1 S a a S S S a a S S S z y x = = − = − = = 5 1 5 , 0 , 5 2 5 2 3 3 3 3 3 3 3 S a a S S S S a a S S z y x = = = − = − = 5 1 5 , 0 , 5 2 5 2 4 4 4 4 4 4 4 S a a S S S S a a S S z y x = = = − = − = 2 Badamy równowagę płyty. Nie znamy sześciu sił w prętach podpierających. Dla przedstawionej na schemacie płyty można zapisać sześć warunków równowagi. Zatem układ jest statycznie wyznaczalny. Równania równowagi są postaci ∑ ∑ ∑ = = = 0 , 0 , 0 iz iy ix P P P ∑ ∑ ∑ = = = 0 , 0 , 0 iz iy ix M M M Kolejność równań jest dowolna. Zatem zapiszemy je tak, aby były one z jedną niewiadomą (jeśli jest to możliwe). Pamiętamy przy tym, że moment siły względem osi jest równy zeru, jeśli wektor siły jest równoległy do osi, linia działania siły przecina się z osią. 0 = ∑ iy P 0 5 2 1 = − S S → 2 5 1 S S = 0 1 = ∑ iy M 0 2 2 2 = − ⋅ − ⋅ Ga a P a S → S S 2 3 2 = 0 1 = ∑ iz M 0 2 5 2 3 = ⋅ a S → 0 3 = S 0 = ∑ ix P 0 5 2 5 2 3 4 = − − S S → 0 4 = S 0 = ∑ ix M 0 5 2 2 5 2 1 . 1 3 5 1 = + ⋅ + + − ⋅ ⋅ − a S a S a S Ga a S → S S 55 . 0 5 = 0 = ∑ iz P 0 5 1 5 1 5 1 4 3 1 6 5 2 = − − + + + + + G S S S S S S S → S S 55 . 0 6 − = Znak minus oznacza, że zwrot wektora siły 6 S jest przeciwny do założonego. W celu sprawdzenia poprawności obliczeń korzystamy z warunku równowagi, z którego nie korzystaliśmy poprzednio 0 = ∑ iz M
... zobacz całą notatkę






Komentarze użytkowników (0)