To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
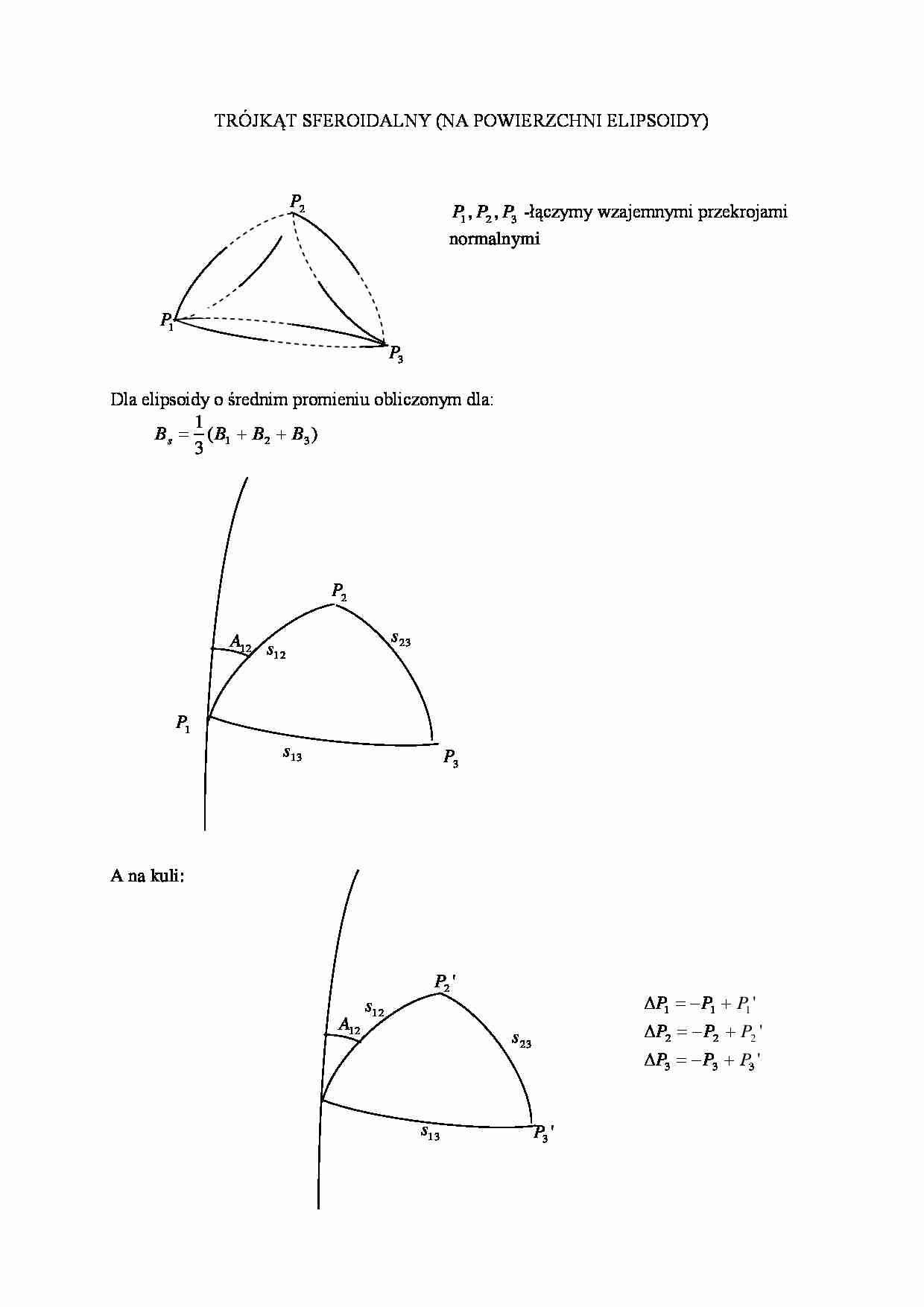

TRÓJKĄT SFEROIDALNY (NA POWIERZCHNI ELIPSOIDY)
P2
P1 , P2 , P3 -łączymy wzajemnymi przekrojami
normalnymi
P1
P3
Dla elipsoidy o średnim promieniu obliczonym dla:
1
Bs ( B1 B2 B3 )
3
P2
s 23
A12 s
12
P1
s13
P3
A na kuli:
P2 '
A12
P1 P1 P1 '
s12
P2 P2 P2 '
s 23
s13
P3 P3 P3 '
P3 '
Istnieją wzory:
sin( A12 A23) sin( A21 A23 )
s12 s 23 s13
s13
s12
12 R
P2 ...
P1
12
2
S
P3 ...
i podstawiamy: s 60km, P1 P2 P3 60
otrzymujemy: P 0,003"
Więc można małe trójkąty sferoidalne obliczać jak sferyczne, a wynikające z tego błędy będą
znacznie mniejsze od dokładności pomiarów.
... zobacz całą notatkę




Komentarze użytkowników (0)