To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
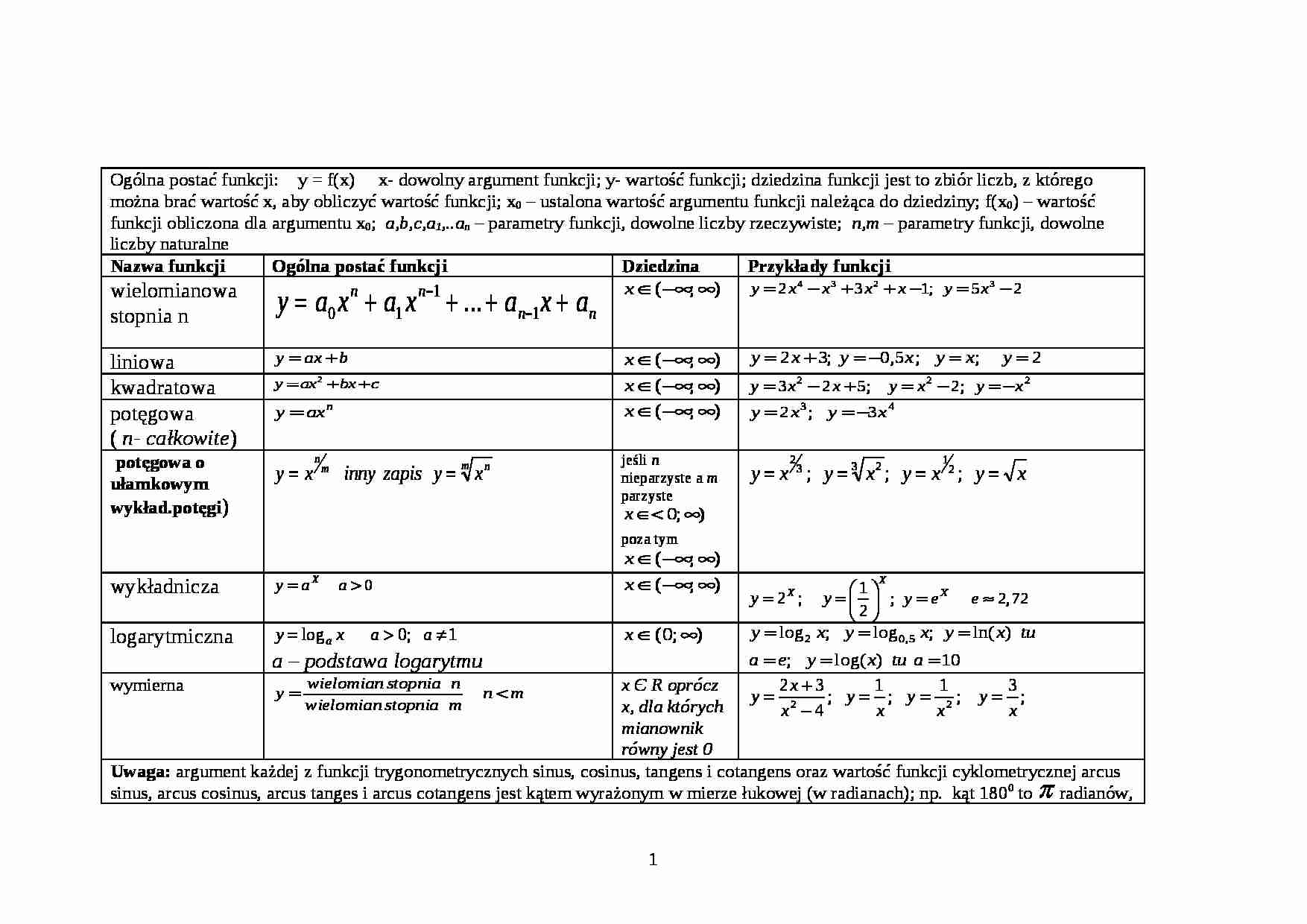


Ogólna postać funkcji: y = f(x) x- dowolny argument funkcji; y- wartość funkcji; dziedzina funkcji jest to zbiór liczb, z którego można brać wartość x, aby obliczyć wartość funkcji; x 0 - ustalona wartość argumentu funkcji należąca do dziedziny; f(x 0 ) - wartość funkcji obliczona dla argumentu x 0 ; a,b,c,a 1 ,..a n - parametry funkcji, dowolne liczby rzeczywiste; n,m - parametry funkcji, dowolne liczby naturalne
Nazwa funkcji Ogólna postać funkcji Dziedzina Przykłady funkcji wielomianowa stopnia n
liniowa
kwadratowa
potęgowa
( n- całkow ite )
potęgowa o ułamkowym wykład.potęgi )
jeśli n nieparzyste a m parzyste poza tym wykładnicza
; logarytmiczna
a - podstawa logarytmu wymierna
x Є R oprócz x, dla których mianownik równy jest 0 Uwaga: argument każdej z funkcji trygonometrycznych sinus, cosinus, tangens i cotangens oraz wartość funkcji cyklometrycznej arcus sinus, arcus cosinus, arcus tanges i arcus cotangens jest kątem wyrażonym w mierze łukowej (w radianach); np. kąt 180 0 to radianów, tzn. w przybliżeniu 3,14 na osi liczbowej OX lub OY a kąt 45 0 to /4 radianów, tj. w przybliżeniu 0,785
Nazwa funkcji Ogólna postać funkcji Dziedzina Zbiór wartości funkcji sinus
y = sin(x)
cosinus
y = cos(x)
tangens
y = tg(x)
cotangens
y=ctg(x)
arcus sinus
y = arc sin(x)
arcus cosinus
y = arc cos(x)
arcus tangens
y = arc tg(x)
arcus cotangens
y = arc ctg(x)
Ogólna postać funkcji: y = f(x) x- dowolny argument funkcji; y- wartość funkcji; dziedzina funkcji jest to zbiór liczb, z którego można brać wartość x, aby obliczyć wartość funkcji; x 0 - ustalona wartość argumentu funkcji należąca do dziedziny; f(x 0 ) - wartość funkcji obliczona dla argumentu x 0 ; a,b,c,a 1 ,..a n - parametry funkcji, dowolne liczby rzeczywiste; n,m - parametry funkcji, dowolne liczby naturalne
Uwaga: argument każdej z funkcji trygonometrycznych sinus, cosinus, tangens i cotangens oraz wartość funkcji cyklometrycznej arcus sinus, arcus cosinus, arcus tanges i arcus cotangens jest kątem wyrażonym w mierze łukowej (w radianach); np. kąt 180
... zobacz całą notatkę






Komentarze użytkowników (0)