To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
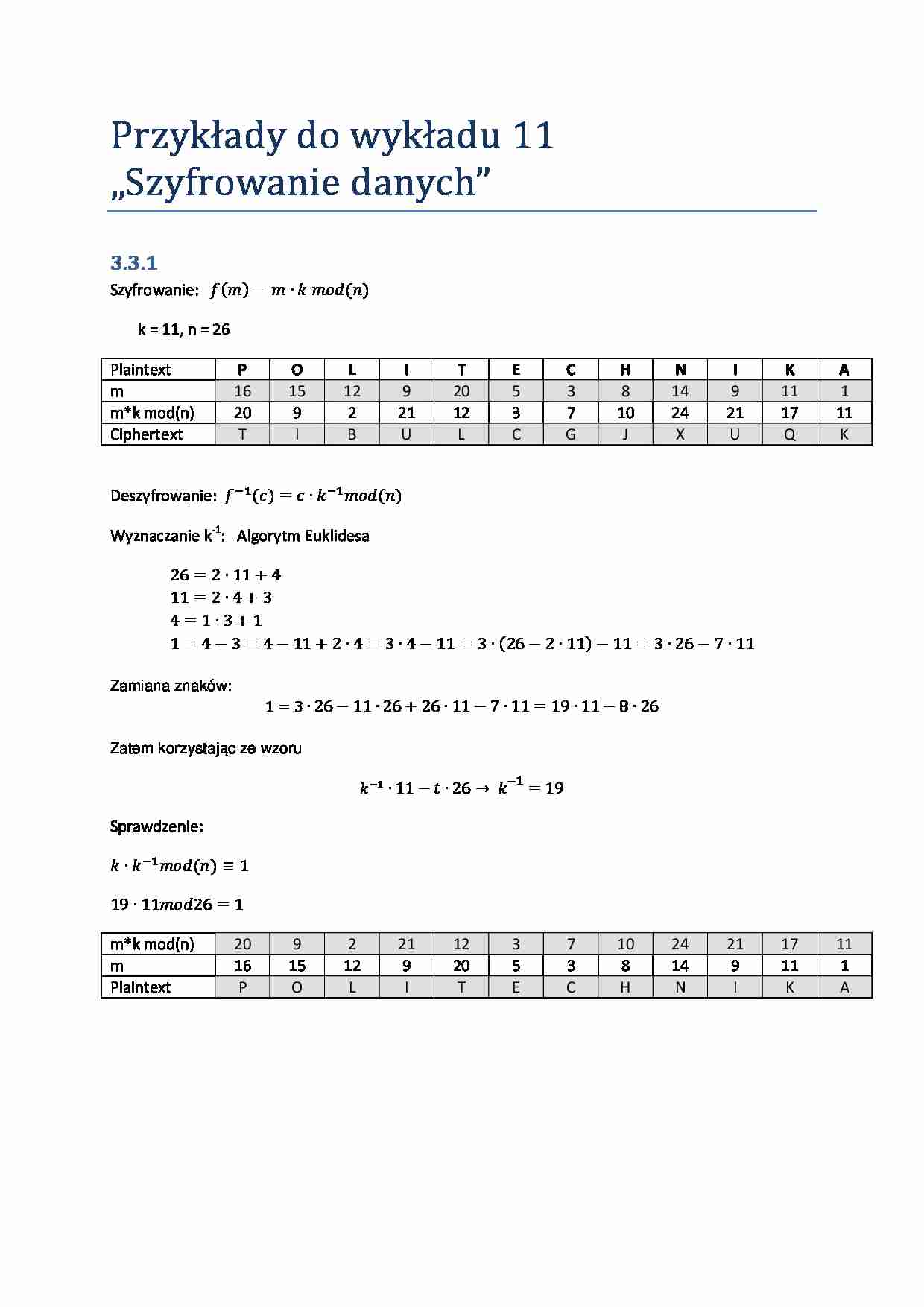


Przykłady do wykładu 11 „Szyfrowanie danych” 3.3.1 Szyfrowanie: ݂ሺ݉ሻ = ݉ ∙ ݇ ݉݀ሺ݊ሻ k = 11, n = 26 Plaintext P O L I T E C H N I K A m 16 15 12 9 20 5 3 8 14 9 11 1 m*k mod(n) 20 9 2 21 12 3 7 10 24 21 17 11 Ciphertext T I B U L C G J X U Q K Deszyfrowanie: ݂ିଵሺܿሻ = ܿ ∙ ݇ିଵ݉݀ሺ݊ሻ Wyznaczanie k -1: Algorytm Euklidesa 26 = 2 ∙ 11 + 4 11 = 2 ∙ 4 + 3 4 = 1 ∙ 3 + 1 1 = 4 − 3 = 4 − 11 + 2 ∙ 4 = 3 ∙ 4 − 11 = 3 ∙ ሺ26 − 2 ∙ 11ሻ − 11 = 3 ∙ 26 − 7 ∙ 11 Zamiana znaków: 1 = 3 ∙ 26 − 11 ∙ 26 + 26 ∙ 11 − 7 ∙ 11 = 19 ∙ 11 − 8 ∙ 26 Zatem korzystając ze wzoru ݇ିଵ ∙ 11 − ݐ ∙ 26 → ݇ −1 = 19 Sprawdzenie: ݇ ∙ ݇ିଵ݉݀ሺ݊ሻ ≡ 1 19 ∙ 11݉݀26 = 1 m*k mod(n) 20 9 2 21 12 3 7 10 24 21 17 11 m 16 15 12 9 20 5 3 8 14 9 11 1 Plaintext P O L I T E C H N I K A 3.3.5 Vigenere TEKST JAWNY A B C D E F G H I J K L M N O P Q R S T U V W X Y Z K L U C Z A A B C D E F G H I J K L M N O P Q R S T U V W X Y Z B B C D E F G H I J K L M N O P Q R S T U V W X Y Z A C C D E F G H I J K L M N O P Q R S T U V W X Y Z A B D D E F G H I J K L M N O P Q R S T U V W X Y Z A B C E E F G H I J K L M N O P Q R S T U V W X Y Z A B C D F F G H I J K L M N O P Q R S T U V W X Y Z A B C D E G G H I J K L M N O P Q R S T U V W X Y Z A B C D E F H H I J K L M N O P Q R S T U V W X Y Z A B C D E
... zobacz całą notatkę






Komentarze użytkowników (0)