To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


A d. 3.2 Tabele parametrów kinematycznych θα manipulator z łokciem
Nr ogniwa
α i a i d i θ i 1
2
3
-pi/2
0
0
0
a 1 a 2 0
0
0
θ 1 *
θ 2 *
θ 3 *
kiść sferyczna
Nr ogniwa
α i a i d i θ i 4
5
6
-pi/2
pi/2
0
0
0 0 0
0
d 6 θ 4 *
θ 5 *
θ 6 *
Ad. 3.3 Modele kinematyczne mani pulatorów manipulator z łokciem
function antropomor(a,q)
L1=link([-pi/2 0 q(1) 0 0])
L2=link([0 a(1) q(2) 0 0])
L3=link([0 a(2) q(3) 0 0])
antropo=robot({L1,L2,L3})
Funkcja wymaga podania - w postaci wektorów - parametrów manipulatora (a jest wektorem długości poszczególnych członów, q zestawem zmiennych konfiguracyjnych).
kiść sferyczna
function nadgarst(d6,q)
L1=link([-pi/2 0 q(1) 0 0])
L2=link([pi/2 0 q(2) 0 0])
L3=link([0 0 q(3) d6 0])
nadgarstek=robot({L1,L2,L3})
Funkcja wymaga podania wartości odsunięcia ostatniego układu współrzędnych związanego z chwytakiem d6 oraz zestawu zmiennych konfiguracyjnych q.
Ad. 3.4 Rozwiązanie zadania prostego kinematyki Po utworzeniu modeli manipulatorów, używamy następujących poleceń:
a) dla manipulatora z łokciem
tr=fkine(antropo,q)
plot(antropo,q)
dla q1=[0 0 0] tr = dla q2=[pi/2 0 pi/2]
tr = dla q3=[-pi 0 pi/2]
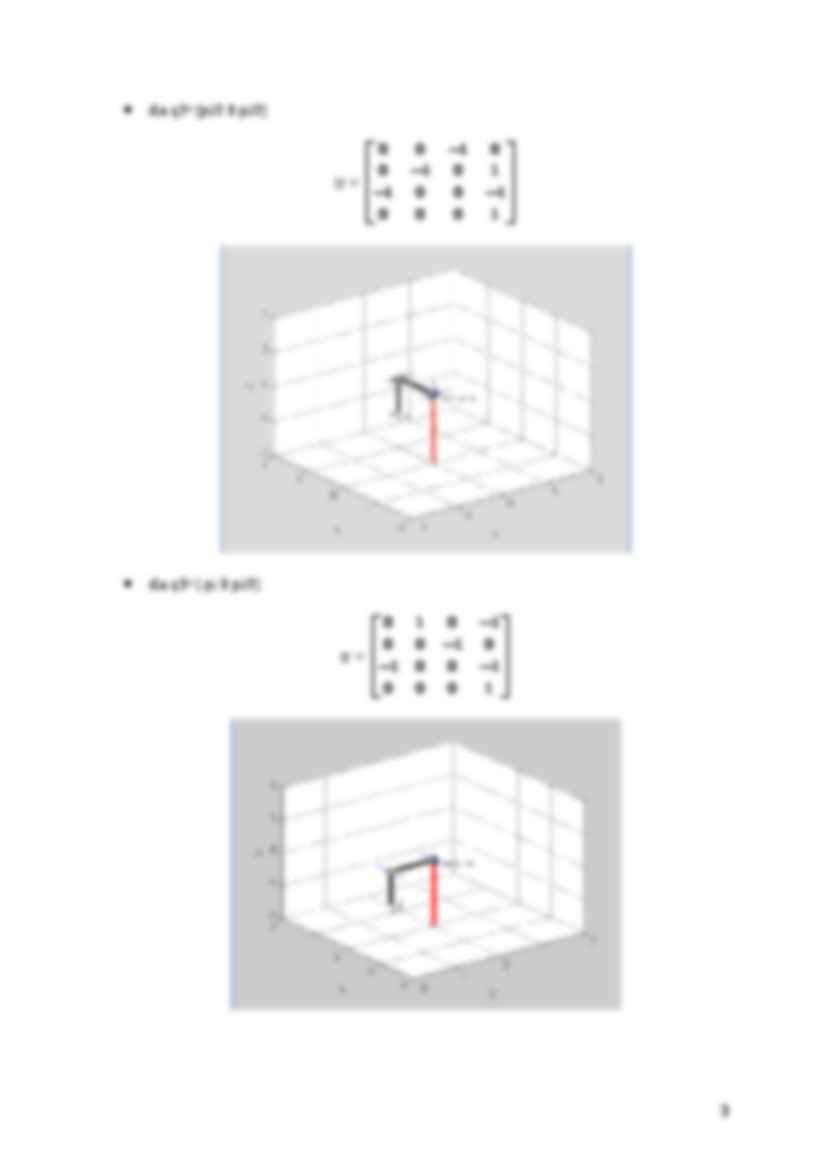
tr = b) dla kiści sferycznej
tr=fkine(nadgarstek,q)
plot(nadgarstek,q)
dla q1=[0 0 0]
tr = dla q2=[pi/2 0 pi/2]
tr = dla q3=[-pi 0 pi/2]
tr = Wyniki otrzymywane dwiema metodami są identyczne.
Ad. 3.5 Macierz trajektorii wielomianowych Użyto następujących poleceń:
... zobacz całą notatkę






Komentarze użytkowników (0)