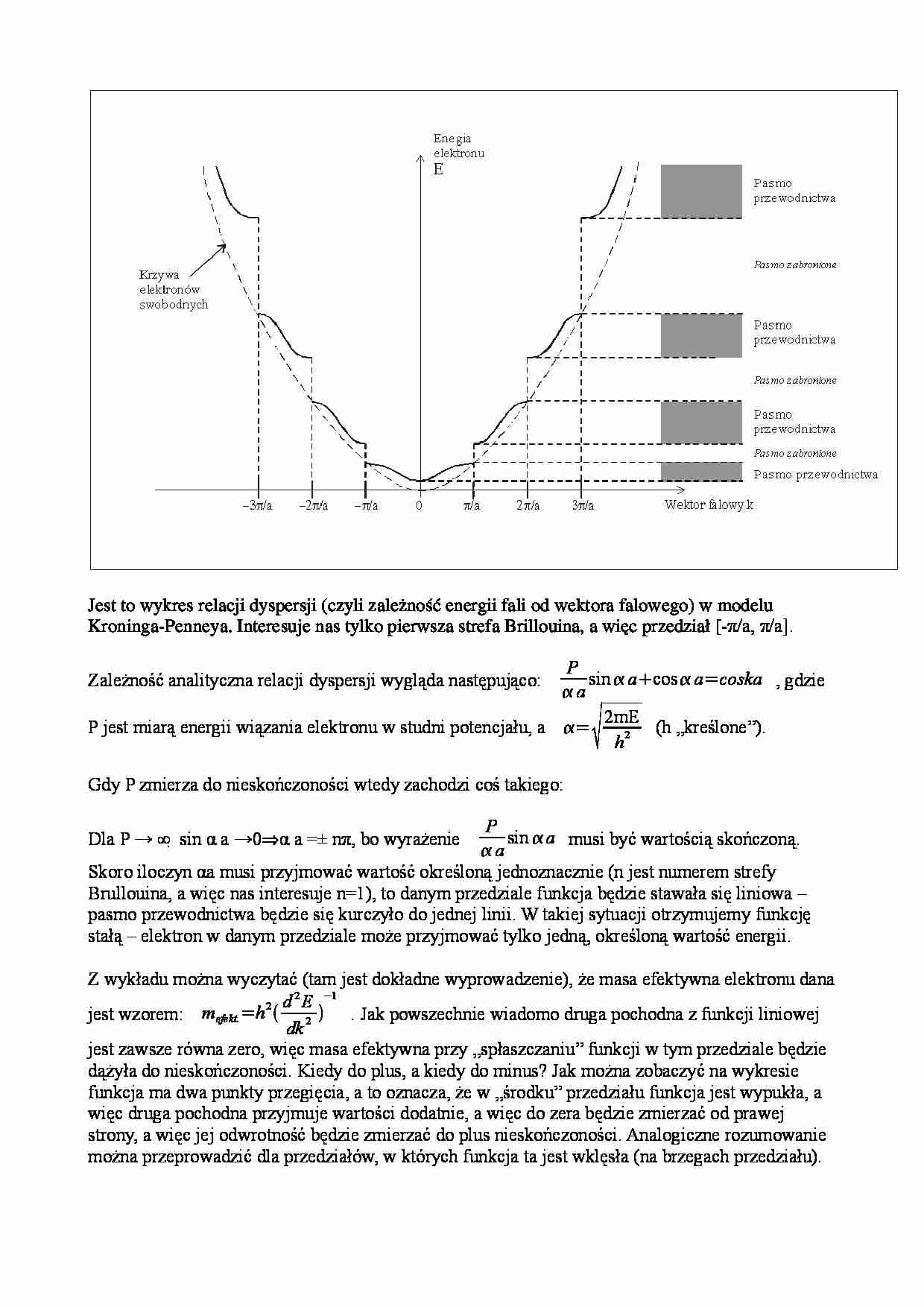
Jest to wykres relacji dyspersji (czyli zale no energii fali od wektora falowego) w modelu ż ść Kroninga-Penneya. Interesuje nas tylko pierwsza strefa Brillouina, a wi c przedzia [- ę ł π/a, π/a]. Zależność analityczna relacji dyspersji wygląda następująco: P a sin a cos a = coska , gdzie P jest miarą energii wiązania elektronu w studni potencjału, a = 2mE h 2 (h „kreślone”). Gdy P zmierza do nieskończoności wtedy zachodzi coś takiego: Dla P → ∞ sin α a →0 α a =± nπ, bo wyrażenie ⇒ P a sin a musi być wartością skończoną. Skoro iloczyn αa musi przyjmować wartość określoną jednoznacznie (n jest numerem strefy Brullouina, a więc nas interesuje n=1), to danym przedziale funkcja będzie stawała się liniowa – pasmo przewodnictwa będzie się kurczyło do jednej linii. W takiej sytuacji otrzymujemy funkcję stałą – elektron w danym przedziale może przyjmować tylko jedną, określoną wartość energii. Z wykładu można wyczytać (tam jest dokładne wyprowadzenie), że masa efektywna elektronu dana jest wzorem: mefekt. = h 2 d 2 E dk 2 − 1 . Jak powszechnie wiadomo druga pochodna z funkcji liniowej jest zawsze równa zero, więc masa efektywna przy „spłaszczaniu” funkcji w tym przedziale będzie dążyła do nieskończoności. Kiedy do plus, a kiedy do minus? Jak można zobaczyć na wykresie funkcja ma dwa punkty przegięcia, a to oznacza, że w „środku” przedziału funkcja jest wypukła, a więc druga pochodna przyjmuje wartości dodatnie, a więc do zera będzie zmierzać od prawej strony, a więc jej odwrotność będzie zmierzać do plus nieskończoności. Analogiczne rozumowanie można przeprowadzić dla przedziałów, w których funkcja ta jest wklęsła (na brzegach przedziału).
... zobacz całą notatkę



Komentarze użytkowników (0)