To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


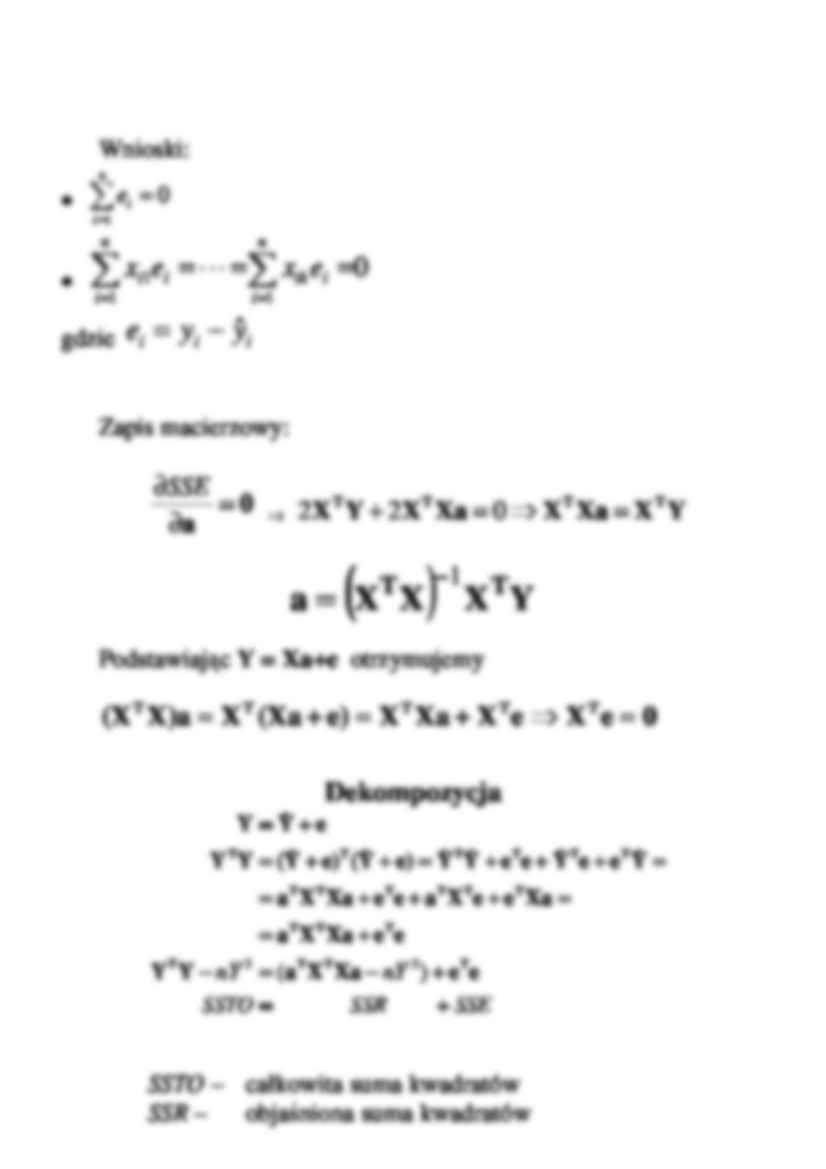
Liniowy model ekonometryczny n i x x Y i ik k i i ,..., 1 ... 1 1 0 = + + + + = ε α α α = n y y y M 2 1 Y = nk n k k x x x x x x L M M M M L L 1 2 21 1 11 1 1 1 X = k α α α M 1 0 α = n ε ε ε M 2 1 ε ε Xα Y + = Klasyczna metoda najmniejszych kwadratów ZałoŜenia: 1. X macierz obserwacji na zmiennych objaśniających jest ustalona 2. 1 ) ( + = k r X (kolumny macierzy X są liniowo niezaleŜne) 3. nk+1 4. n i D E i i ,..., 1 ) ( , 0 ) ( 2 2 = = = σ ε ε (homoskedastyczność) 5. j i ,...,n , i,j j i ≠ = = 2 1 0 ) , cov( ε ε 6. Zaburzenia losowe są niezaleŜne od zmiennych objaśniajacych Kryterium najmniejszych kwadratów: min 2 ) ˆ ( 1 2 1 2 → + − = = − − = = = = = − = ∑ ∑ = = Xa X a Y X a Y Y Xa) (Y Xa) (Y e e T T T T T T T n i i n i i i e y y SSE gdzie [ ] Xa Y = = = n i i y ,..., 1 ˆ ˆ [ ] k 1,2,..., i = = i a a - estymator wektora parametrów α Xa Y e − = - wektor reszt Układ równań normalnych: = ∂ ∂ = ∂ ∂ = ∂ ∂ 0 0 0 1 0 k a SSE a SSE a SSE L ⇔ = + − − − ∂ ∂ = + − − − ∂ ∂ = + − − − ∂ ∂ ∑ ∑ ∑ = = = n i ik k i i k n i ik k i i n i ik k i i x a x a a y a x a x a a y a x a x a a y a 1 2 1 1 0 1 2 1 1 0 1 1 2 1 1 0 0 0 ) ... ( 0 ) ... ( 0 ) ... ( K = = =
(…)
…
nowych zmiennych objaśniających.
Skorygowany R2
SSE ( n − k − 1)
R = 1−
SSTO ( n − 1) .
2
WNIOSKOWANIE STATYSTYCZNE W
MODELU REGRESJI WIELORAKIEJ
E (a) = E[( X T X)−1 X T Y ] = E[( X T X)−1 X T ( Xα + ε )] =
= α + ( X T X)− 1 X T E (ε ) = α
Przy załoŜeniu, Ŝe E (ε ) = 0 estymator KMNK jest
nieobciąŜonym estymatorem wektora parametrów α .
Macierz wariancji-kowariancji:
[
]
= E[(a − α)(a − α ) ] =
D…
... zobacz całą notatkę




Komentarze użytkowników (0)