To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
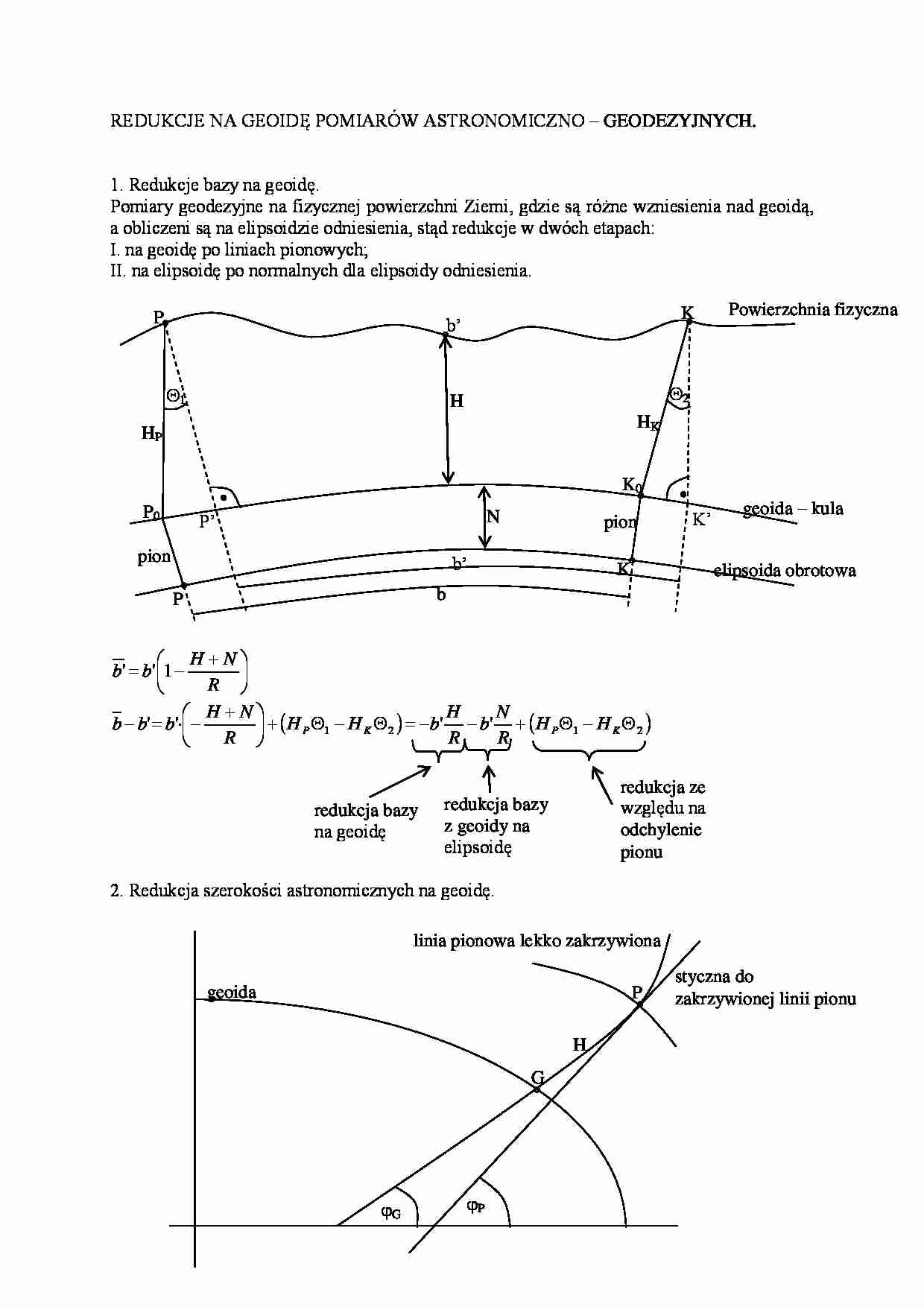


REDUKCJE NA GEOIDĘ POMIARÓW ASTRONOMICZNO – GEODEZYJNYCH.
1. Redukcje bazy na geoidę.
Pomiary geodezyjne na fizycznej powierzchni Ziemi, gdzie są różne wzniesienia nad geoidą,
a obliczeni są na elipsoidzie odniesienia, stąd redukcje w dwóch etapach:
I. na geoidę po liniach pionowych;
II. na elipsoidę po normalnych dla elipsoidy odniesienia.
P
K
b’
1
Powierzchnia fizyczna
2
H
HK
HP
K0
P0
N
P’
pion
pion
b’
K’
K
geoida – kula
elipsoida obrotowa
b
P
HN
b' b' 1
R
H
N
HN
b b' b'
H P 1 H K 2 b' b' H P 1 H K 2
R
R
R
redukcja bazy
na geoidę
redukcja ze
względu na
odchylenie
pionu
redukcja bazy
z geoidy na
elipsoidę
2. Redukcja szerokości astronomicznych na geoidę.
linia pionowa lekko zakrzywiona
geoida
P
H
G
G
P
styczna do
zakrzywionej linii pionu
Przez punkt P na wysokości H nad geoidą poprowadzona jest linia siły ciężkości (wklęsła ku
biegunowy) i przecina ona geoidę w punkcie G. Kierunek prostej pionowej w pkt. P różni się
od kierunku prostej pionowej w pkt. G. Zatem kąty jakie tworzą te proste z płaszczyzną
równika, czyli szerokości P , G są różne. Wyprowadza się wzór:
H
G P sin 2 dla R=6371km, =0,0053
R
G P
H sin 2
H
G P
albo
sin 2
6
1"
5830m
1202 10 m
Redukcja równa się 0 dla =90 i =0 (biegun i równik), ponieważ linie sił są tam proste.
Dla =45 redukcja jest największa, dla H=5830m redukcja wyniosła by 1”.
1” – 30m
0,1” – 3m
3. Redukcje azymutu astronomicznego.
3.1 Redukcja azymutu ze względu na wzniesienie celu ponad geoidę.
normalna w
S
B”– stanowisko instrumentu (na geoidzie elipsoidy)
pkt. P
A’
P – cel na wysokości H nad geoidą
”
P
P’ – rzut normalny pkt. P na geoidę
S
H
BS, BP’ – łuki południków punktów P i S
P’ P”
Ns,NP – przecięcia normalnych z S i P z osią figury,
A
normalne s i p są wichrowate.
Ns
NP
Prowadząc przez Ns i P płaszczyznę normalną otrzymamy przekrój normalny SP”, którego
azymut A’=BSP” jest azymutem zmierzonym. Wyprowadza się :
e2 H
e2
1
A A'
cos 2 sin 2 A' gdzie
0,''108
2a
2a
km
np. dla H=1km max redukcji wynosi 0,11”.
Ponieważ azymut obarczony jest większymi błędami obserwacyjnymi, to jeśli cel nie był
bardzo wysoko często redukcję można zaniedbać.
3.2 Redukcja azymutu ze względu na wzniesienie stanowiska.
linia pionu
(zakrzywiona)
prosta styczna
pow.
ekwipotencjalna
P
H
’
geoida
P” P’
B
P – stanowisko na wysokości H nad geoidą;
P’ – rzut punktu P po linii pionu;
P” – rzut punktu P po stycznej do linii pionu;
- azymut zredukowany;
’ – azymut zmierzony punktu B (kąt pionowy z P)
wtedy:
H
' tgh sin 2 sin ' .
R
Przeważnie h w sieciach poziomych jest małe i redukcję można zaniedbać. Dodatkowo jeśli
celowa znajduje się w płaszczyźnie południka to redukcja równa się 0.
4. Redukcja kątów poziomych na geoidę.
P’K
PK
S’
K
S
Kąt poziomy
(wszystkie
punkty nad
geoidą)
PL
K’
Rzut na
geoidę
P’L
Kąt poziomy jest różnicą azymutów:
... zobacz całą notatkę






Komentarze użytkowników (0)