To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
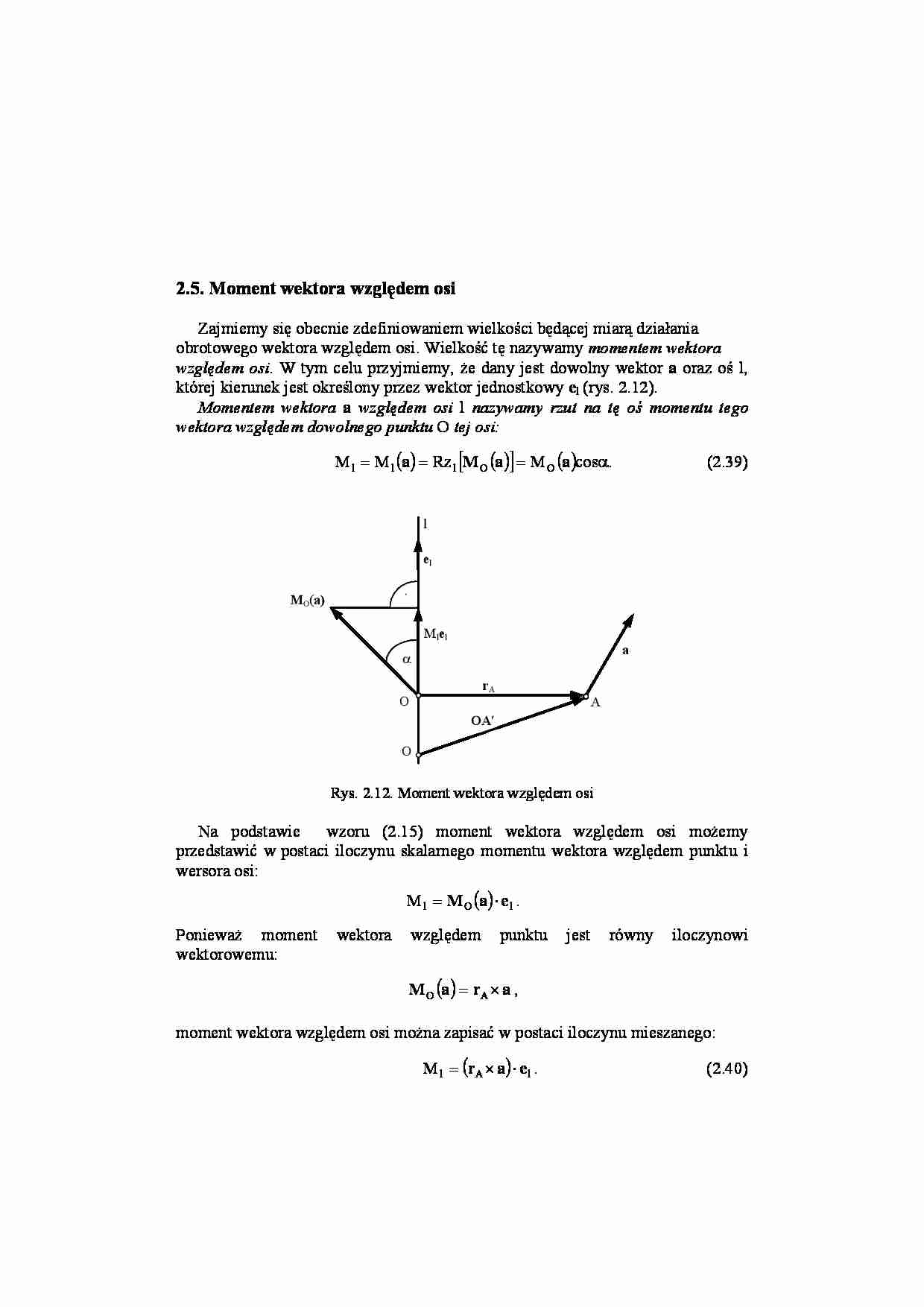


2.5. Moment wektora względem osi Zajmiemy się obecnie zdefiniowaniem wielkości będącej miarą działania obrotowego wektora względem osi. Wielkość tę nazywamy momentem wektora względem osi . W tym celu przyjmiemy, że dany jest dowolny wektor a oraz oś l, której kierunek jest określony przez wektor jednostkowy e l (rys. 2.12). Momentem wektora a względem osi l nazywamy rzut na tę oś momentu tego wektora względem dowolnego punktu O tej osi: ( ) ( ) [ ] ( ) . cos M Rz M M O O l l l α = = = a a M a (2.39) OA ′ l e l a A O O r A M O( a) α ⋅ Ml e l Rys. 2.12. Moment wektora względem osi Na podstawie wzoru (2.15) moment wektora względem osi możemy przedstawić w postaci iloczynu skalarnego momentu wektora względem punktu i wersora osi: ( ) l O l M e a M ⋅ = . Ponieważ moment wektora względem punktu jest równy iloczynowi wektorowemu: ( ) a r a M × = A O , moment wektora względem osi można zapisać w postaci iloczynu mieszanego: ( ) l A l M e a r ⋅ × = . (2.40) Tak zdefiniowany moment wektora względem osi jest skalarem. Definicja ta jest wystarczająca, ponieważ wektor ( ) l l M e a jest skierowany wzdłuż osi l, przeto do jego opisu wystarczy podanie tylko jego wartości. Aby podana na wstępie definicja momentu względem osi była jednoznaczna, należy wykazać, że rzut na oś l momentu wektora a względem punktu O leżącego na tej osi nie zależy od położenia punktu O na tej osi. W tym celu obliczymy moment wektora a względem innego punktu ′ O leżącego na osi l (rys. 2.12) i dokonamy jego rzutu na tę oś: ( ) [ ] ( ) Rz l O O M a M a e ′ ′ = l ⋅ . (a) Na podstawie rys. 2.12 wektor ′ O A możemy przedstawić jako sumę wektora : ′ O O r i A . A r O O A O + ′ = ′ Po podstawieniu tej zależności do wzoru (a) oraz skorzystaniu z własności iloczynu mieszanego otrzymamy: ( ) [ ] ( ) [ ] ( ) ( ) ( ) ( ) ( ) Rz l O l l l A l l A l M a O O r a e O O a r a e O O a e r a e e O O a r a e A A ′ = ′ + × ⋅ = ′ × + × ⋅ = = ′ × ⋅ + × ⋅ = × ′ ⋅ + × ⋅ . Ponieważ wektory są równoległe, ich iloczyn wektorowy jest równy zeru: e O e O O l i ′
... zobacz całą notatkę






Komentarze użytkowników (0)