To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
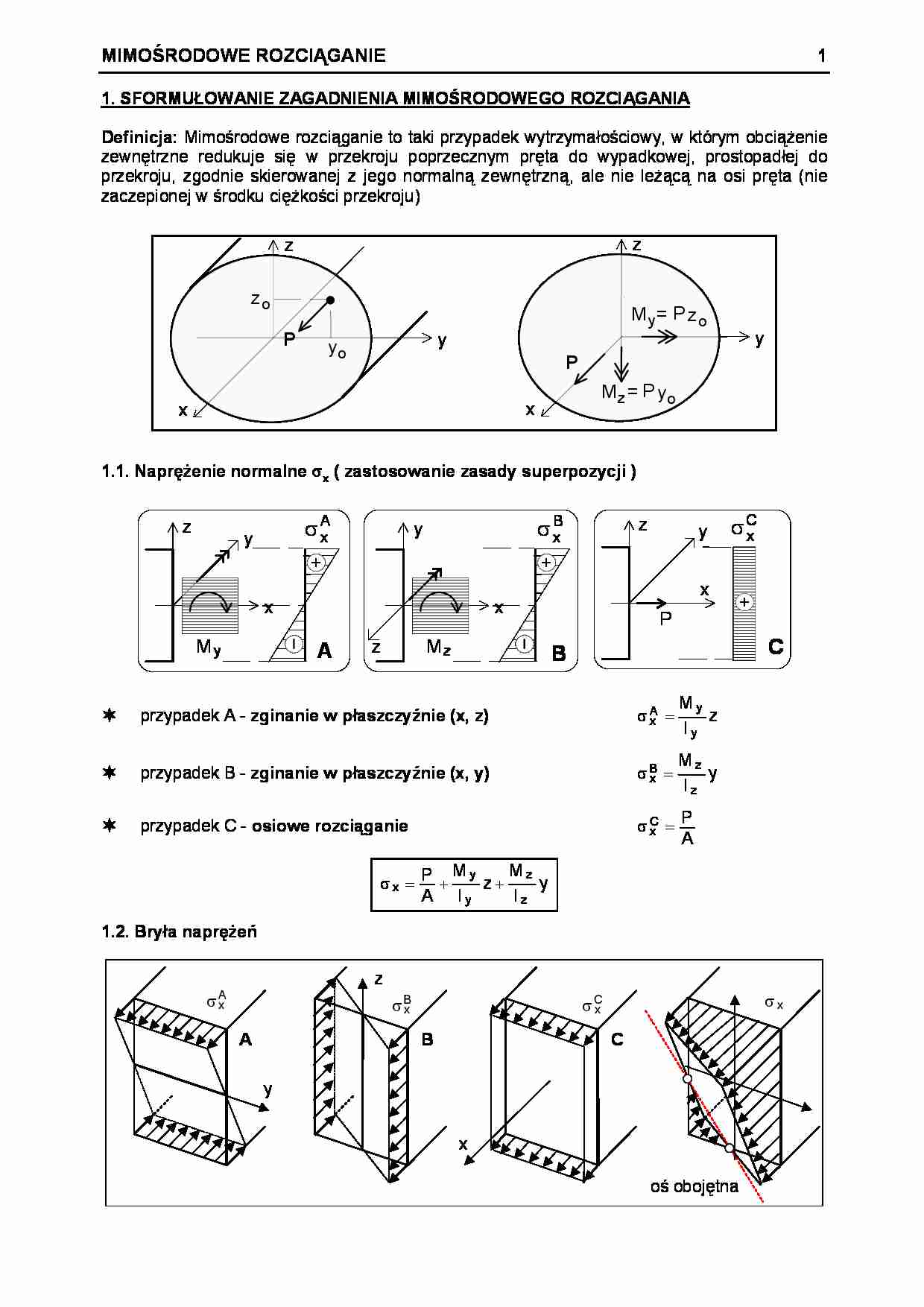


MIMOŚRODOWE ROZCIĄGANIE 1 1. SFORMUŁOWANIE ZAGADNIENIA MIMOŚRODOWEGO ROZCIĄGANIA Definicja: Mimośrodowe rozciąganie to taki przypadek wytrzymałościowy, w którym obciążenie zewnętrzne redukuje się w przekroju poprzecznym pręta do wypadkowej, prostopadłej do przekroju, zgodnie skierowanej z jego normalną zewnętrzną, ale nie leżącą na osi pręta (nie zaczepionej w środku ciężkości przekroju) y z x P o y o z y z x P P o z y M = z M = P o y 1.1. Naprężenie normalne σ x ( zastosowanie zasady superpozycji ) + x y z My A σ x A y B + x z Mz σ x B σ x C x y z P C + przypadek A - zginanie w płaszczyźnie (x, z) σ xA y y M I z = przypadek B - zginanie w płaszczyźnie (x, y) σ xB z z M I y = przypadek C - osiowe rozciąganie σ xC P A = σ x y y z z P A M I z M I y = + + 1.2. Bryła naprężeń y A σxA z B σ xB x C σxC oś obojętna σ x MIMOŚRODOWE ROZCIĄGANIE 2 1.3. Oś obojętna Definicja: oś obojętna to zbiór punktów, w których naprężenie σx osiąga wartość zerową. σx y y z z P A M I z M I y = + + = 0 P A P z I z P y I y A P o y o z = − − × 1 = − + − z I A z y I A y y o z o i I A i I A y y z z 2 2 = = y a z a y z + = 1 a i y a i z y def z o z def y o = − = − 2 2 1.4. Własności osi obojętnej y z y a 0 0 1 1 z a o P ( y , z ) o o P ( y , z ) 1 1 1 oś obojętna zawsze przechodzi przez "ćwiartkę" układu współrzędnych, przeciwną do tej, w której działa siła ( yo , zo 0 ⇒ ay , az
(…)
… lub całkowicie poza jego obszarem
oznacza, że naprężenia w całym przekroju muszą być tego samego znaku ( skoro na osi
obojętnej wynoszą one zero, to po jednej ze stron osi muszą być dodatnie, a po drugiej
ujemne).
Definicja :
Rdzeń przekroju to miejsce geometryczne położenia punktów, w których działająca siła
powoduje powstanie w przekroju naprężeń jednakowego znaku.
1.6. Własności rdzenia przekroju
Rdzeń…
... zobacz całą notatkę






Komentarze użytkowników (0)