To tylko jedna z 17 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
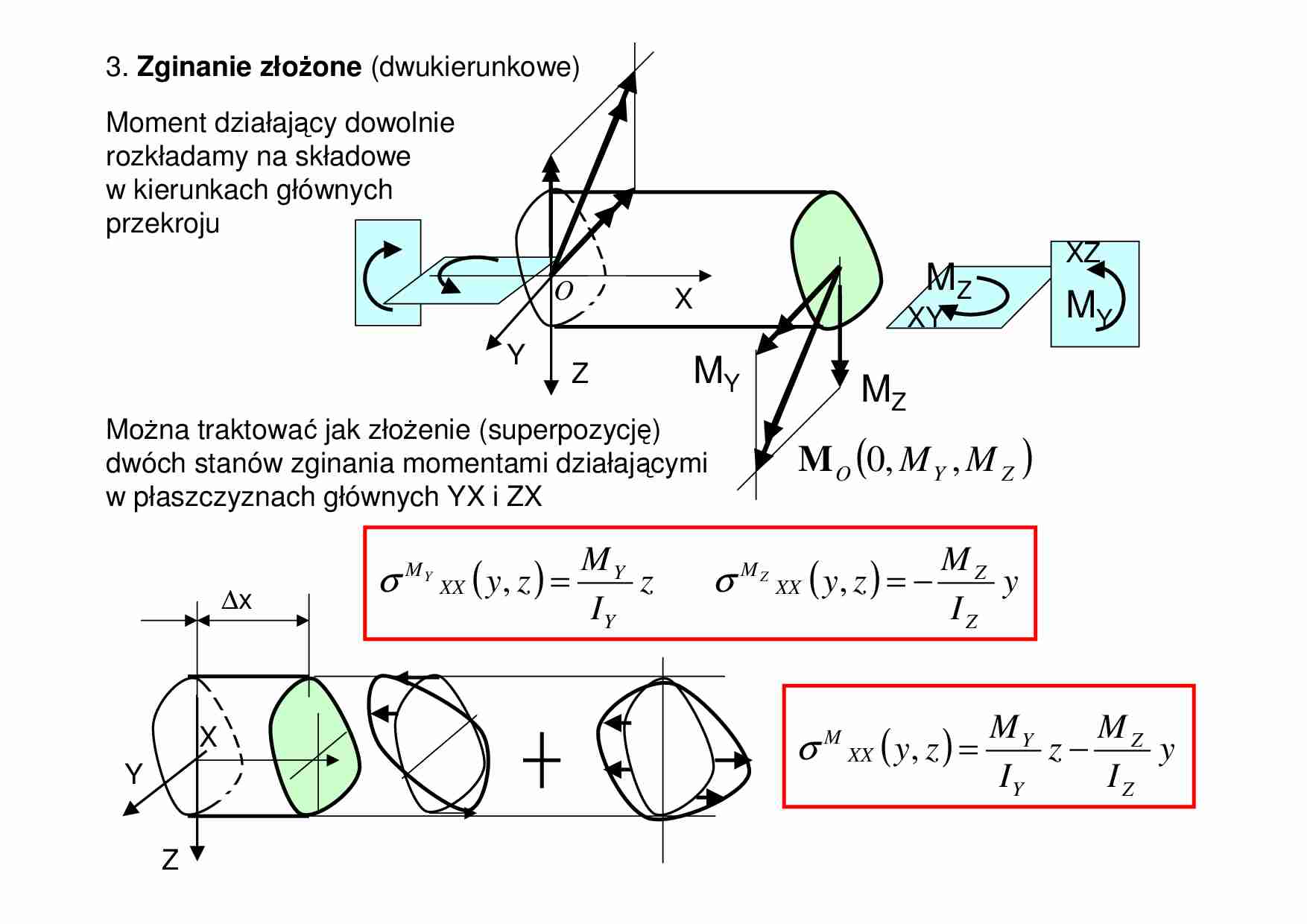
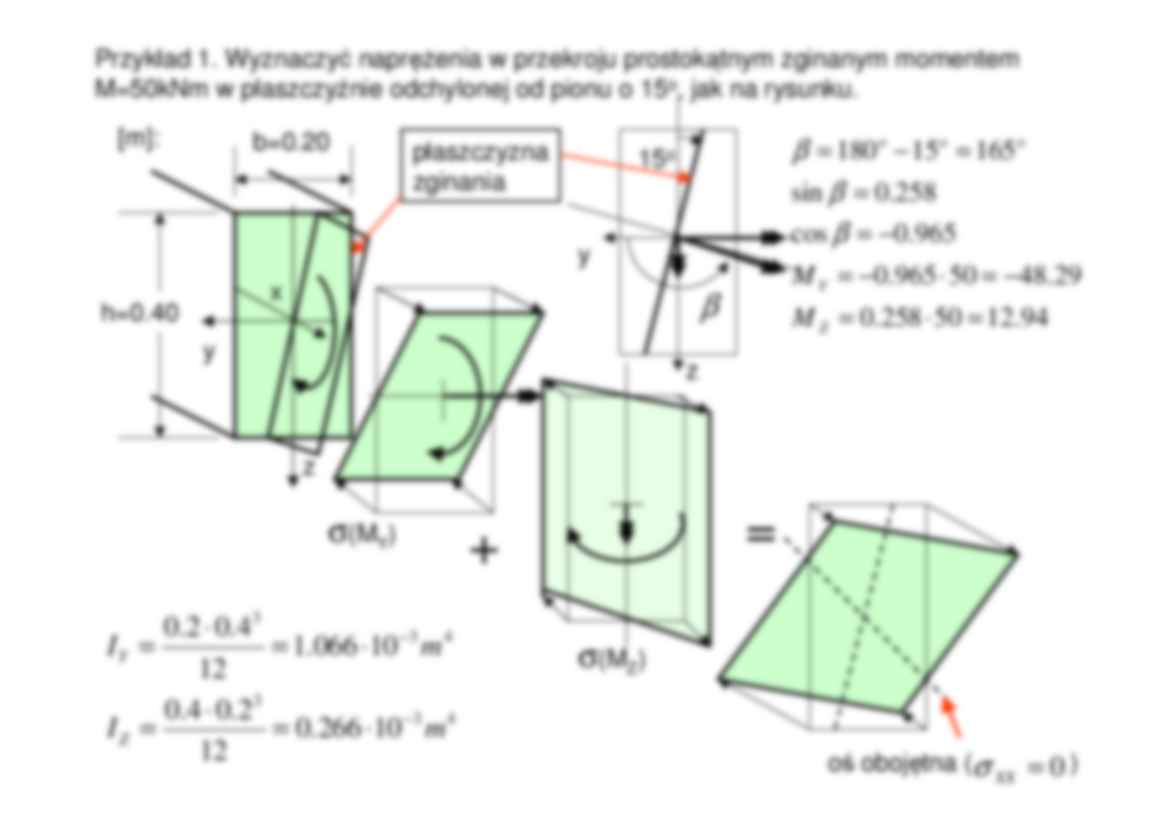

3. Zginanie złoŜone (dwukierunkowe) M Y M Z XZ XY X Y Z M Y M Z ( ) Z Y O M M , , 0 M O MoŜna traktować jak złoŜenie (superpozycję) dwóch stanów zginania momentami działającymi w płaszczyznach głównych YX i ZX ( ) z I M z y Y Y XX M Y = , σ ( ) y I M z y Z Z XX M Z − = , σ ∆x X Y Z ( ) y I M z I M z y Z Z Y Y XX M − = , σ Moment działający dowolnie rozkładamy na składowe w kierunkach głównych przekroju Przykład 1. Wyznaczyć napręŜenia w przekroju prostokątnym zginanym momentem M=50kNm w płaszczyźnie odchylonej od pionu o 15o, jak na rysunku. x y z + h=0.40 b=0.20 [m]: 4 3 3 4 3 3 10 266 . 0 12 2 . 0 4 . 0 10 066 . 1 12 4 . 0 2 . 0 m I m I Z Y − − ⋅ = ⋅ = ⋅ = ⋅ = 94 . 12 50 258 . 0 29 . 48 50 965 . 0 965 . 0 cos 258 . 0 sin 165 15 180 = ⋅ = − = ⋅ − = − = = = − = Z Y o o o M M β β β y z 15o β płaszczyzna zginania oś obojętna ( ) 0 = XX σ = σ(M Y) σ(M Z) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) MPa MPa MPa MPa MPa MPa MPa MPa m m kNm y I M z I M z y XX XX XX XX Z Z Y Y XX 135 . 4 852 . 4 987 . 8 " 1 . 0 266 . 0 94 . 12 ) 2 . 0 ( 066 . 1 29 . 48 2 . 0 , 1 . 0 83 . 13 852 . 4 987 . 8 " ) 1 . 0 ( 266 . 0 94 . 12 ) 2 . 0 ( 066 . 1 29 . 48 2 . 0 , 1 . 0 135 . 4 852 . 4 987 . 8 " ) 1 . 0 ( 266 . 0 94 . 12 2 . 0 066 . 1 29 . 48 2 . 0 , 1 . 0 83 . 13 852 . 4 987 . 8 10 1 . 0 266 . 0 94 . 12 2 . 0 066 . 1 29 . 48 2 . 0 , 1 . 0 , 4 3 = − = = − − ⋅ − − − = − = + = = − − ⋅ − − − − = − − − = + − = = − − ⋅ − − − = − − = − − = = ⋅ ⋅ − − = − = − σ σ σ σ σ 13.83 -13.83 -4.135 4.135 ( ) : ] [ MPa M XX σ bryła napręŜeń Przykład 2. Belka wspornikowa wykonana z L90x60x8, długości 2m została obciąŜona siłą P=1.5kN. Wyznaczyć napręŜenia w punktach A,B,C.
(…)
…
dla dowolnego kierunku, wynik identyczny, stąd rdzeń jest równieŜ kołem
Przykład 3 Wypadkowa sił wewnętrznych działających na słup
50 murowany przechodzi przez p.K i wnosi N = -800kN
[cm]: z (siła ściskająca). Znaleźć:
a) rozkład napręŜeń (bryłę napręŜeń) i oś obojętną
25 b) rdzeń przekroju
y
Do a) i b)
40 K 1.Powierzchnia i środek cięŜkości
43.6
20
F = 0.25⋅ 0.40 + 0.25⋅ 0.50 = 0.225 m2
0.25⋅ 0.40⋅ 0.20…
…
h2
2
iZ
h
*
eZ 2 = − = − 12 = −
h
c2
6
2
Koło:
F = πR 2 , I Z =
z
o1
R
−
4
4
,
πR 4
P1
R
πR 4
y
IZ
R2
2
,
iZ =
= 42 =
4
F πR
o1 :
y=R
b1 = R, c1 = ∞,
R2
2
*
e = − iZ = − 4 = − R
Y1
4
b1
R
*
eZ 1 = 0
dla dowolnego kierunku, wynik identyczny, stąd rdzeń jest równieŜ kołem
Przykład 3
[cm]:
Wypadkowa sił wewnętrznych działających na słup
murowany przechodzi przez p.K i wnosi N…
… obojętnej
postaci odcinkowej (przekształcone)
z (patrz geometria analityczna)
* *
y z eY eZ
+ =1 ⇔ − 2 y − 2 z =1
b c iZ iY
c
2
iZ
y z b = − e*
⇒ + =1⇒ Y
iZ iY
2 2 2
iY
c = − *
y − *
e − *
e
Y Z
eZ
o
b * 2
P (e *Y , e *Z ) iZ
eY = − b współrzędne punktu
⇒ 2
przyłoŜenia siły odpowiadające
połoŜeniu osi obojętnej danemu
eZ = −
* iY
przez b i c
c
Wyznaczamy…
... zobacz całą notatkę






Komentarze użytkowników (0)