To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


MIARY DYSPERSJI.
Miary dyspersji (zmienności, rozproszenia) charakteryzują stopień zróżnicowania jednostek zbiorowości
pod względem badanej cechy.
Miary zmienności dzielimy na:
- klasyczne
- pozycyjne
Wariancja,
Odchylenie standardowe
Odchylenie przeciętne
Klasyczny współczynnik zmienności
Rozstęp,
Odchylenie ćwiartkowe
Pozycyjny współczynnik zmienności
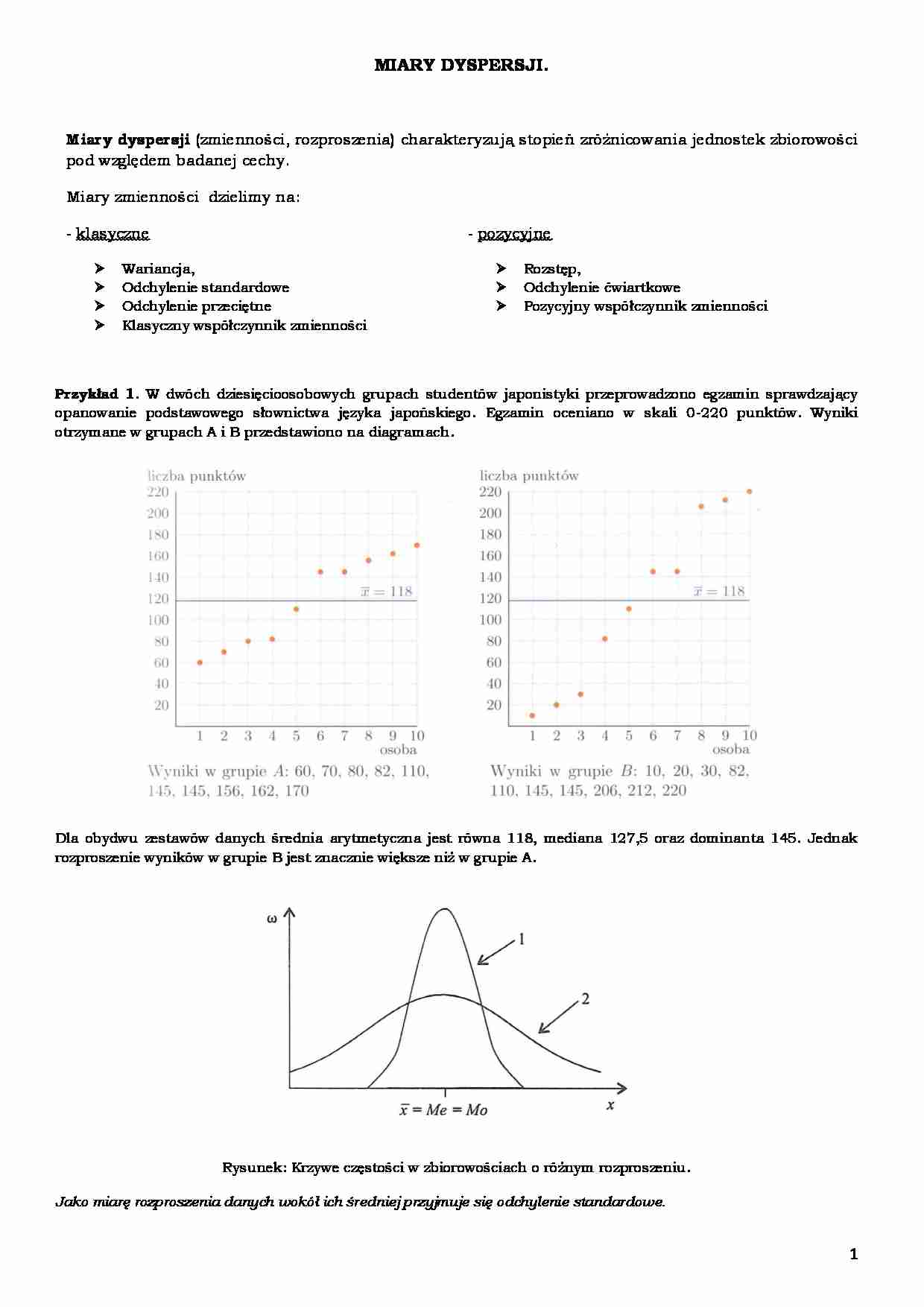
Przykład 1. W dwóch dziesięcioosobowych grupach studentów japonistyki przeprowadzono egzamin sprawdzający
opanowanie podstawowego słownictwa języka japońskiego. Egzamin oceniano w skali 0-220 punktów. Wyniki
otrzymane w grupach A i B przedstawiono na diagramach.
Dla obydwu zestawów danych średnia arytmetyczna jest równa 118, mediana 127,5 oraz dominanta 145. Jednak
rozproszenie wyników w grupie B jest znacznie większe niż w grupie A.
Rysunek: Krzywe częstości w zbiorowościach o różnym rozproszeniu.
Jako miarę rozproszenia danych wokół ich średniej przyjmuje się odchylenie standardowe.
1
Miary klasyczne:
1.
Wariancja ( ) – średnia arytmetyczna kwadratów odchyleń poszczególnych wartości cechy od średniej
arytmetycznej zbiorowości.
Dla danych niepogrupowanych
Dla danych pogrupowanych w szereg rozdzielczy punktowy:
Dla danych pogrupowanych w szereg rozdzielczy przedziałowy:
2.
Odchylenie standardowe: (s) – miara zróżnicowania o mianie zgodnym z mianem badanej cechy, określa
przeciętne zróżnicowanie poszczególnych wartości cechy od średniej arytmetycznej;
(pierwiastek z wariancji).
Typowy obszar zmienności – w tym obszarze mieszczą się wartości cechy około 2/3 wszystkich jednostek
badanej zbiorowości statystycznej; określony jest wzorem:
Z odchyleniem standardowym wiąże się tzw. reguła trzech sigm, która mówi, ze wystąpienie obserwacji o
wartości cechy poza przedziałem
jest mało prawdopodobne. W przypadku rozkładów o
niewielkiej asymetrii tylko około 1/3 obserwacji wykracza poza typowy przedział zmienności, a tylko 5%
obserwacji – poza przedział
.
Rysunek: Graficzna prezentacja reguły trzech sigm.
Innymi słowy:
2
3.
Odchylenie przeciętne: (d) – średnia arytmetyczna bezwzględnych odchyleń wartości cechy od jej średniej
arytmetycznej; określa ono, o ile jednostki danej zbiorowości różnią się średnio, ze względu na wartości
cechy, od średniej arytmetycznej;
Dla danych niepogrupowanych
Dla danych pogrupowanych w szereg rozdzielczy punktowy :
Dla danych pogrupowanych w szereg rozdzielczy przedziałowy :
Miary pozycyjne:
1.
Rozstęp
– empiryczny obszar zmienności badanej cechy, nie daje on informacji o zróżnicowaniu
poszczególnych wartości cechy w zbiorowości.
2.
Odchylenie ćwiartkowe – określa odchylenie wartości cechy od mediany; jest to połowa różnicy między
trzecim a pierwszym kwartylem; mierzy poziom zróżnicowania tylko części jednostek, a mianowicie:
pozostałej po odrzuceniu 25% jednostek o wartościach najmniejszych i 25% jednostek o wartościach
największych
Typowy obszar zmienności – w tym obszarze mieszczą się wartości cechy około 2/3 wszystkich jednostek
(…)
…. przyniosła wyniki zaprezentowane
w tabeli. Obliczyć s.
Oszczędności w tys. zł
Oszczędzający
0-4
10
4-8
120
8-12
100
12-16
90
16-20
40
7. Instytut Meteorologii i Gospodarki Wodnej zanotował temperaturę w ciągu kolejnych dni kwietnia 1999r. w
Warszawie:
Temperatura w C
0
2
6
8
13
15
17
20
23
25
27
Liczba dni
2
3
3
4
5
6
2
2
1
1
1
a) Obliczyć odchylenie przeciętne temperatury kolejnych dni w kwietniu.
b…
…. przyniosła wyniki zaprezentowane
w tabeli. Obliczyć s.
Oszczędności w tys. zł
Oszczędzający
0-4
10
4-8
120
8-12
100
12-16
90
16-20
40
7. Instytut Meteorologii i Gospodarki Wodnej zanotował temperaturę w ciągu kolejnych dni kwietnia 1999r. w
Warszawie:
Temperatura w C
0
2
6
8
13
15
17
20
23
25
27
Liczba dni
2
3
3
4
5
6
2
2
1
1
1
a) Obliczyć odchylenie przeciętne temperatury kolejnych dni w kwietniu.
b…
... zobacz całą notatkę






Komentarze użytkowników (0)