To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
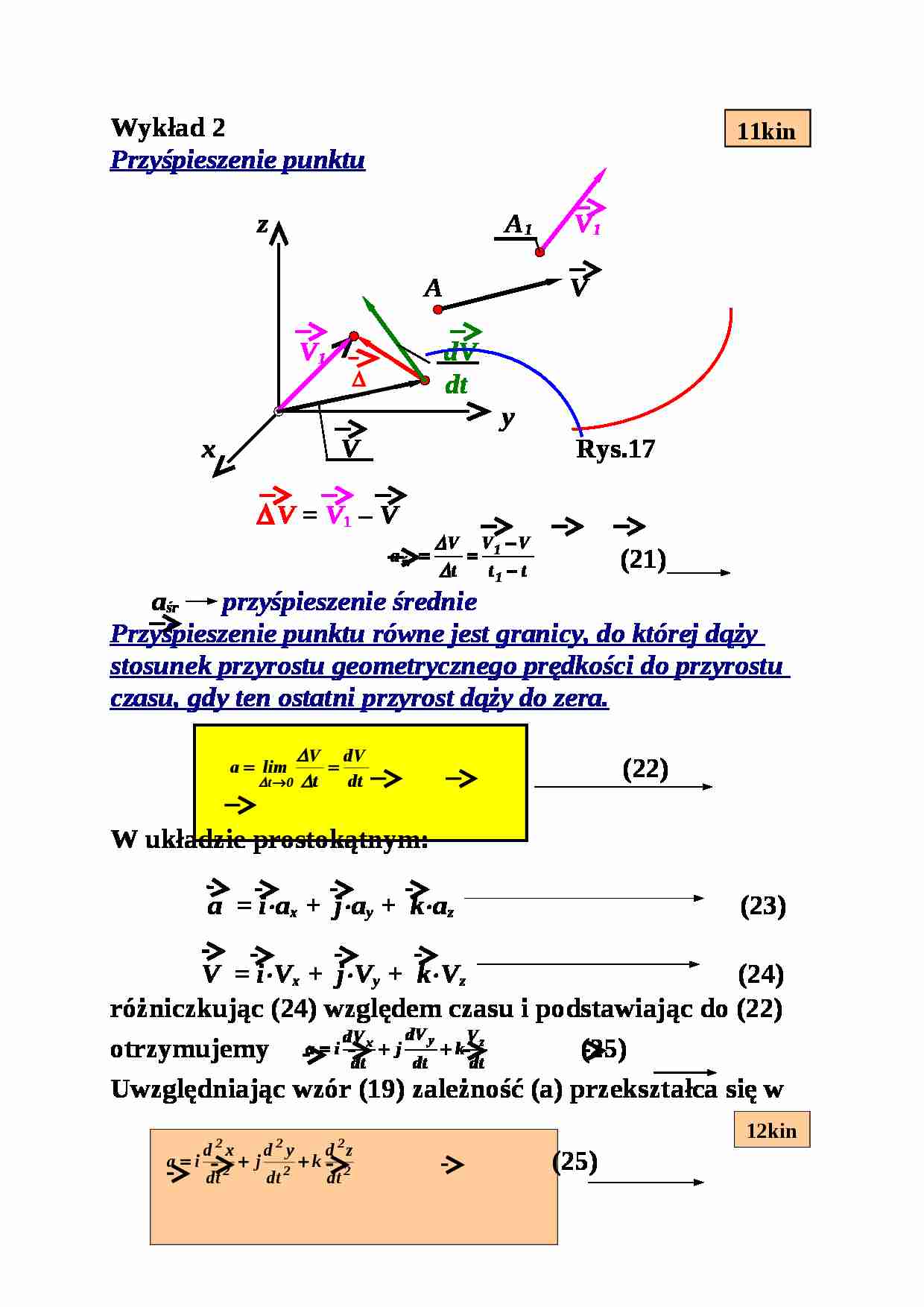


Wykład 2 Przyśpieszenie punktu z A 1 V 1 A V V 1 dV dt y x V Rys.17 Δ V = V 1 - V (21) a śr przyśpieszenie średnie Przyśpieszenie punktu równe jest granicy, do której dąży stosunek przyrostu geometrycznego prędkości do przyrostu czasu, gdy ten ostatni przyrost dąży do zera. (22) W układzie prostokątnym: a = i ⋅ a x + j ⋅ a y + k ⋅ a z (23) V = i ⋅ V x + j ⋅ V y + k ⋅ V z (24) różniczkując (24) względem czasu i podstawiając do (22) otrzymujemy (25) Uwzględniając wzór (19) zależność (a) przekształca się w (25) Porównując (23) z (25) otrzymujemy (26) Wartość bezwzględna przyśpieszenia: (27) Przykład 4 Należy wyznaczyć przyśpieszenie punktu A poruszającego się w płaszczyźnie Oxy , którego równania ruchu mają postać: (b) a, b, k oznaczają tu pewne stałe. Rozwiązanie Torem punktu A jest elipsa (patrz przykład 3), zgodnie ze wzorem (26) składowe przyśpieszenia mają postacie: Wartość bezwzględna przyśpieszenia wynosi: gdzie r oznacza długość promienia elipsy (rys18) y V A x 0A = r
(…)
…, określający kierunek prostej Różniczkując względem czasu t promień wektor r, otrzymujemy wektor prędkości V (c)
stąd wartość bezwzględna (29)
Różniczkując względem czasu wektor prędkości V otrzymujemy wektor przyśpieszenia a
(30) Ruch jednostajny V = ds/dt = const
czyli ds = V⋅dt (d)
Po scałkowaniu zależności (d) w przedziale odpowiadającym punktom M0 i M, przy założeniu, że to = 0
i OM0 = so otrzymujemy: stąd s
s1 V
V=const
α
so 0 t1 t t1 t
Rys. 20 Wykresy drogi i prędkości w ruchu jednostajnym
prostoliniowym
Ruch jednostajnie zmienny czyli całkujemy to równanie
uwzględniając (19) mamy (e)
całkując (e) otrzymujemy:
(f)
Jeśli a>0 to ruch jednostajnie przyśpieszony,
jeśli a<0 to ruch jednostajnie opóźniony
s V a
s
so V0 ds. a
t1 t s t t
0 t dt t1
Rys.21 Wykresy drogi, prędkości i przyśpieszenia w ruchu jednostajnie przyśpieszonym
Przykład 5
Równanie ruchu punktu poruszającego się po linii prostej ma postać
gdzie: s droga w m, t czas w s. Wyznaczyć prędkość V i przyśpieszenie a punktu dla t = 4 s.
Rozwiązanie
prędkość przyśpieszenie po podstawieniu do powyższych równań czasu t = 4 s
, Ruch harmoniczny prosty
(31)
b, ω, *o są stałymi
x odległość punktu M od punktu O zwanego środkiem
ruchu harmonicznego (rys.22) b amplituda ruchu harmonicznego
* = ω⋅t +*o faza ruchu harmonicznego
*o faza początkowa ruchu harmonicznego
-b b
M2 0 M0 a M V M1
bsin*0 t = 0
x
Rys.22 Ruch harmoniczny prosty punktu
prędkość punktu M przyśpieszenie punktu M Ponieważ funkcja sin(kt+*0) jest funkcją okresową badany ruch punktu (31) jest także ruchem okresowym, tzn. powtarzającym się w równych odstępach czasu. Okres T tego ruchu, czyli najkrótszy przedział czasu, po którego upływie punkt powróci do położenia, które zajmował w chwili t, poruszając się w tę samą stronę. Warunek stąd
(32)
częstość ruchu Hz (33)
ω rad / s-1 pulsacja lub częstość kołowa
Przykład 6
Punkt M porusza się ruchem harmonicznym po prostej l
z przyśpieszeniem . W chwili początkowej dla t = to = 0: x = x0 = 0, V = .
Wyznaczyć funkcję prędkości V(t) i odległość…
... zobacz całą notatkę






Komentarze użytkowników (0)