Drgania harmoniczne-opracowanie - Ruch harmoniczny

Nasza ocena:

3
Pobrań: 322
Wyświetleń: 1288
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
Drgania harmoniczne-opracowanie - Ruch harmoniczny - strona 1 Drgania harmoniczne-opracowanie - Ruch harmoniczny - strona 2 Drgania harmoniczne-opracowanie - Ruch harmoniczny - strona 3

Fragment notatki:

Drgania harmoniczne
O oscylatorze harmonicznym możemy mówić wtedy, kiedy siła hamująca działa proporcjonalnie do wychylenia z położenia
równowagi. Równanie ruchu ma wtedy postać:
d 2x
2
 0 x  0
2
dt
Pierwszy wyraz to zapisane różniczkowo przyśpieszenie ciała a. W drugim wyrazie występuje wychylenie x oraz częstość
drgań własnych 0. Rozwiązanie takiego równania ma postać:
x  A sin 0t   
gdzie f – faza początkowa. Są to drgania okresowe, a okres drgań wynosi
Przykładem drgań harmonicznych jest ruch odważnika o masie m, zaczepionego do nieważkiej
sprężyny o współczynniku sprężystości k. Równanie ruchu ma postać:
ma  kx
d 2x
m 2  kx
dt
gdzie x- wydłużenie sprężyny
Porównując to równanie z równaniem oscylatora
harmonicznego otrzymujemy
częstość drgań własnych:
0 
k
m
T
2
0
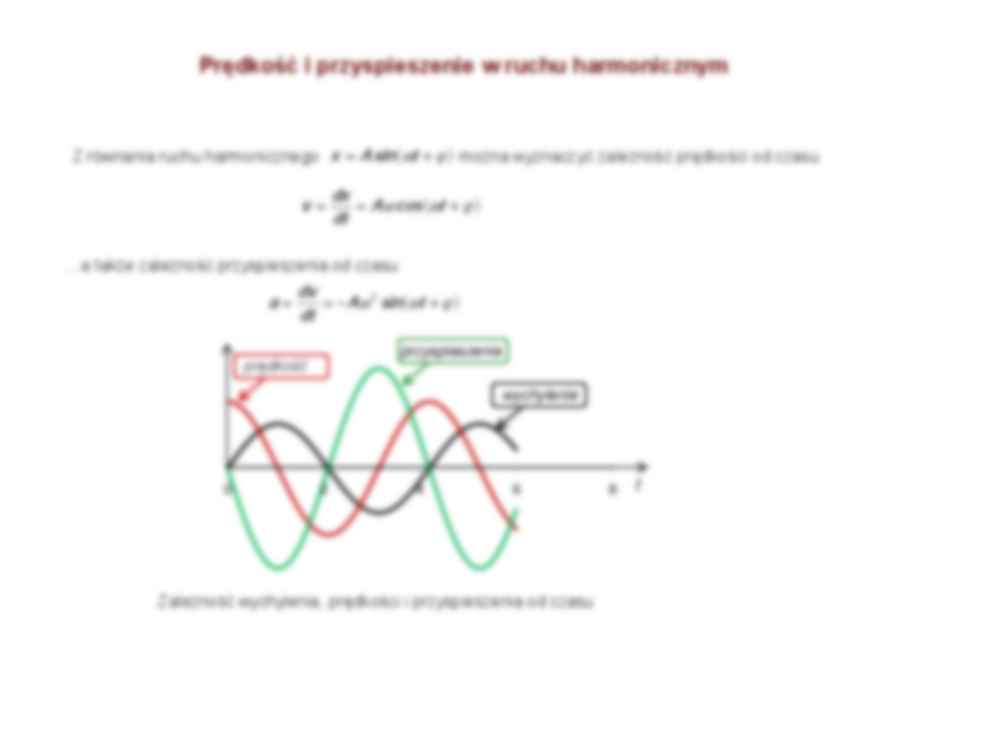
Prędkość i przyspieszenie w ruchu harmonicznym
Z równania ruchu harmonicznego x  A sin t    można wyznaczyć zależność prędkości od czasu
v 
dx
 A cos t   
dt
…a także zależność przyspieszenia od czasu
a
dv
 A 2 sin t   
dt
przyspieszenie
prędkość
wychylenie
0
2
4
6
Zależność wychylenia, prędkości i przyspieszenia od czasu
8
t
Energia w ruchu harmonicznym
Energię potencjalną w ruchu harmonicznym wyznaczamy, obliczając pracę, jaką trzeba wykonać, aby przesunąć ciało
na odległość x z położenia równowagi. Przy przesuwaniu o odcinek dx wykonamy pracę:
dW  Fdx
x
x
0
0
W   Fdx    kx dx 
Całkowita praca jest równa:
kx 2
2
Ep 
Energia potencjalna w ruchu harmonicznym:
Energia kinetyczna w ruchu harmonicznym: E k 
mv 2
2

kx 2
2
m 2 A 2 cos t   
2
Energia całkowita w ruchu harmonicznym:
Ec  E p  Ek 
kx 2
2

mv 2
2

kA 2 sin 2 t    m 2 A 2 cos 2 t   
Energia całkowita nie zależy od czasu – jest stała

2
Ec 
2
kA 2

kA 2
2
E
2
Ec 
kA 2
2
Zależność energii kinetycznej i potencjalnej od wychylenia
Ek 
Ep 
mv 2
2
0
x
kx 2
2
Wahadło matematyczne i fizyczne
Równanie ruchu dla wahadła matematycznego ma postać:
ma  mg sin 
Po przeliczeniu przyśpieszenia liniowego na kątowe, oraz zastosowaniu przybliżenia sin a =
a dla małych kątów, otrzymujemy:
g
  0
l
gdzie  – przyśpieszenie kątowe, lub
w zapisie różniczkowym:
d 2 g
  0
2
l
dt
Jest to równanie oscylatora harmonicznego, którego okres i częstotliwość wynoszą

g
l
T  2
l
g
Podobne obliczenia można przeprowadzić dla bryły sztywnej, zawieszonej na osi
przechodzącej powyżej swojego środka masy. Otrzymujemy:
I  mgd  0
T  2
I
mgd
gdzie I – moment bezwładności bryły względem wybranej
osi, m – masa bryły, g – przyśpieszenie ziemskie, d –
odległość od wybranej osi do środka masy bryły.
Drgania harmoniczne
Zadanie 1.
Długość swobodna sprężyny zwisającej pionowo wynosi L0 = 10 cm, a jej stała sprężystości k wynosi 100 N/m. Na sprężynie
zawieszono kulkę o masie m = 1 kg a następnie puszczono swobodnie. Oblicz, jakie będzie najniższe i najwyższe położenie
kulki. Podaj, gdzie ... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz