

Fragment notatki:
5.2.1. Tor, prędkość i przyśpieszenie punktu
Rozpatrzmy ruch punktu materialnego względem przyjętego układu odniesienia
uważanego za nieruchomy. Aby poznać ruch tego punktu, w każdej chwili musimy
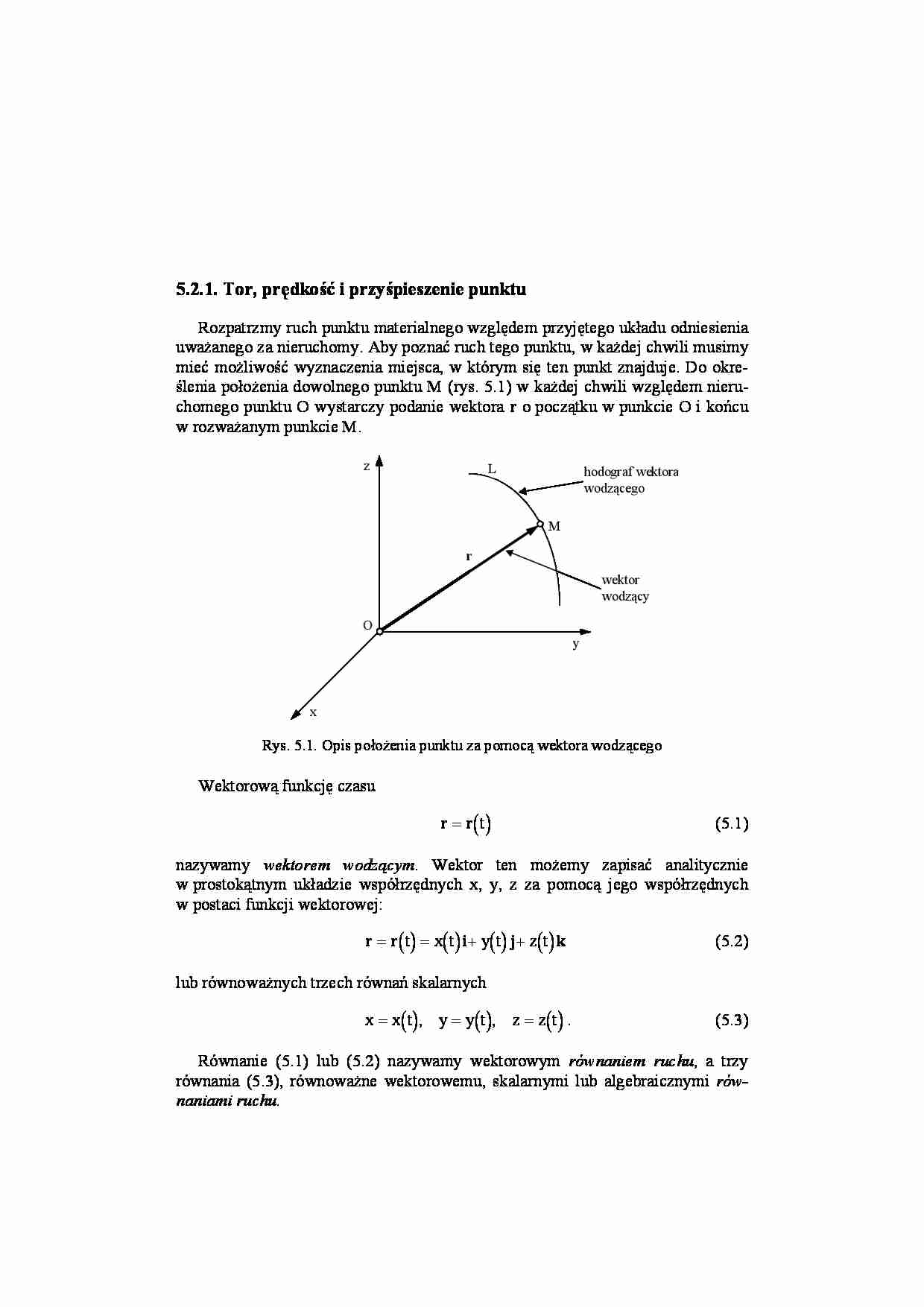
mieć możliwość wyznaczenia miejsca, w którym się ten punkt znajduje. Do określenia położenia dowolnego punktu M (rys. 5.1) w każdej chwili względem nieruchomego punktu O wystarczy podanie wektora r o początku w punkcie O i końcu
w rozważanym punkcie M.
z
L
hodograf wektora
wodzącego
M
r
wektor
wodzący
O
y
x
Rys. 5.1. Opis położenia punktu za pomocą wektora wodzącego
Wektorową funkcję czasu
r = r( t )
(5.1)
nazywamy wektorem wodzącym. Wektor ten możemy zapisać analitycznie
w prostokątnym układzie współrzędnych x, y, z za pomocą jego współrzędnych
w postaci funkcji wektorowej:
r = r( t ) = x( t ) i + y( t ) j+ z( t ) k
(5.2)
lub równoważnych trzech równań skalarnych
x = x( t ), y = y( t ), z = z( t ) .
(5.3)
Równanie (5.1) lub (5.2) nazywamy wektorowym równaniem ruchu, a trzy
równania (5.3), równoważne wektorowemu, skalarnymi lub algebraicznymi równaniami ruchu.
91
Gdy punkt M będzie się poruszał, wektor r będzie zmieniał z upływem czasu
swoją wartość i kierunek, a koniec tego wektora zakreśli krzywą L, którą będziemy
nazywać torem punktu lub hodografem wektora wodzącego r. Jak już powiedziano
w p. 2.3.7, hodograf rozpatrywanej funkcji wektorowej to linia zakreślona przez
końce wektorów, których początki znajdują się w jednym punkcie.
W czasie ruchu punktu M wektor wodzący r tego punktu będzie zmieniał swoją
wartość i kierunek. Załóżmy, że w chwili czasu t1 położenie punktu M1 wyznacza
wektor wodzący r1 = r(t1), a w chwili t2 = t1 + ∆t punkt zajmuje położenie M2 wyznaczone przez wektor wodzący r2 = r(t2), jak na rys. 5.2. Widzimy, że po upływie
czasu ∆t = t2 – t1 wektor wodzący uzyskał przyrost ∆r = r2 – r1. Iloraz ∆r/∆t jest
wektorem współliniowym z wektorem ∆r, czyli jest skierowany wzdłuż cięciwy
M1M2. Jeżeli przyrost czasu ∆t będzie dążył do zera, to w granicy otrzymamy pochodną wektora r względem czasu:
lim
∆t →0
∆r dr
=
= v,
dt
∆t
nazywaną prędkością punktu. Oznacza to, że prędkością punktu nazywamy
pochodną względem czasu wektora wodzącego tego punktu:
v=
z
dr
.
dt
(5.4)
M1
L
v=
∆r
r1
dr
dt
M2
r2
∆r
∆t
O
y
x
Rys. 5.2. Prędkość punktu
Łatwo zauważyć, że jeżeli punkt M2 dąży do punktu M1, to cięciwa M1M2 dąży
do stycznej do toru w punkcie M1. Wynika stąd, że prędkość punktu jest styczna do
toru punktu M, czyli styczna do hodografu wektora wodzącego r.
92
Gdy wektor wodzący zapiszemy w postaci (5.2), to zgodnie z podanymi
w p. 2.3.7 zasadami różniczkowania jego pochodna
v=
d r dx dy dz
=
i+
j+ k .
dt dt
dt
dt
(5.5)
Po zapisaniu prędkości v w układzie współrzędnych x, y, z
v = v x i + v y j+ v z k
(5.6)
i podstawieniu do równania (5.5) oraz po porównaniu wyrazów przy tych samych
wersorach otrzymamy wzory na współrzędne prędkości:
vx =
dx
dy
dz
, vy =
, vz =
.
dt
dt
dt
(5.7)
Widzimy, że współrzędne prędkości
(…)
… granicę ilorazu przyrostu wektora wodzącego ∆r i przyrostu
drogi ∆l
95
∆r dr
=
,
∆l
dl
to otrzymamy pochodną wektora wodzącego r względem drogi l. Moduł tej pochodnej jest równy jedności, ponieważ gdy ∆l będzie dążyć do zera, to długość
cięciwy MM′ = ∆r będzie dążyć do długości łuku ∆l:
lim
∆ →0
lim
∆l→0
∆r
dr
=
= 1.
∆l
dl
Zatem pochodna wyrażona wzorem:
es =
dr
dl
jest równa wersorowi stycznej es…
… do M′ doznał przyrostu ∆es. Jeżeli zbudujemy wektor będący ilorazem przyrostu ∆es i długości łuku ∆l i wyznaczymy
granicę tej wielkości przy ∆l dążącym do zera, to otrzymamy drugą pochodną wektora wodzącego r względem drogi l:
∆ es d es d 2 r
=
= 2 .
∆l→0 ∆l
dl
dl
lim
(a)
96
Kierunek tego wektora będzie normalny do krzywej w punkcie M, ponieważ jeżeli
punkt M′ będzie się zbliżał do punktu M, to kąt między przyrostem ∆es i wersorem
es będzie dążył do kąta prostego. Można to też wykazać analitycznie. Wiadomo, że
iloczyn wersora pomnożonego skalarnie przez siebie będzie równy jedności:
e s ⋅ e s = 1.
Po zróżniczkowaniu tej zależności względem czasu mamy:
es ⋅
d e dl
d es
= 0 lub e s ⋅ s
= 0,
dl dt
dt
a po podzieleniu przez dl/dt
es ⋅
d es
d2 r
= es ⋅ 2 = 0 .
dl
dl
Z powyższego wynika, że druga pochodna wektora wodzącego względem drogi
jest wektorem prostopadłym do osi stycznej s.
Wyznaczymy obecnie moduł drugiej pochodnej wektora wodzącego r względem drogi l. Z rysunku 5.5 można zauważyć, że dla małych przyrostów ∆r trójkąt
es ∆es e ′ i trójkąt N M M′ są podobne. Możemy zatem napisać:
s
∆ es
e
= s .
∆r
MN
Wiadomo także, że gdy ∆l będzie dążyć do zera, to długość przyrostu ∆r będzie
dążyć do długości łuku ∆l…
…, czyli ⏐∆r⏐ = ∆l. Powyższą równość zapiszemy zatem
w postaci:
∆ es
e
= s ,
∆l
MN
a po obliczeniu granicy tej równości mamy:
∆ es
e
d es
d2 r
1
1
=
=
= s =
= ,
2
∆l→0 ∆l
dl
MN MN ρ
dl
lim
ponieważ z geometrii analitycznej wiadomo, że granica:
lim M ′N = ρ
M ′→ M
jest promieniem krzywizny, czyli promieniem koła ściśle stycznego w rozpatrywanym punkcie.
97
Ostatecznie moduł drugiej pochodnej wektora wodzącego…
… prędkością kątową ω = π s−1 .
Wyznaczyć prędkość i przyśpieszenie trzpienia dla czasu t1 = 0,5 s, jeżeli oś
trzpienia pokrywa się z osią x tak jak na rysunku.
Rozwiązanie. Dla obliczenia prędkości i przyśpieszenia trzpienia musimy ułożyć jego równanie ruchu, np. równanie punktu A. Na podstawie rys. 5.7b możemy
napisać:
x A = OA = OD + DA = e cosϕ + r 2 − CD 2 =
= e cosϕ + r 2 − ( e sinϕ ) = e cosϕ + r 2 − e…
... zobacz całą notatkę

Komentarze użytkowników (0)