To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

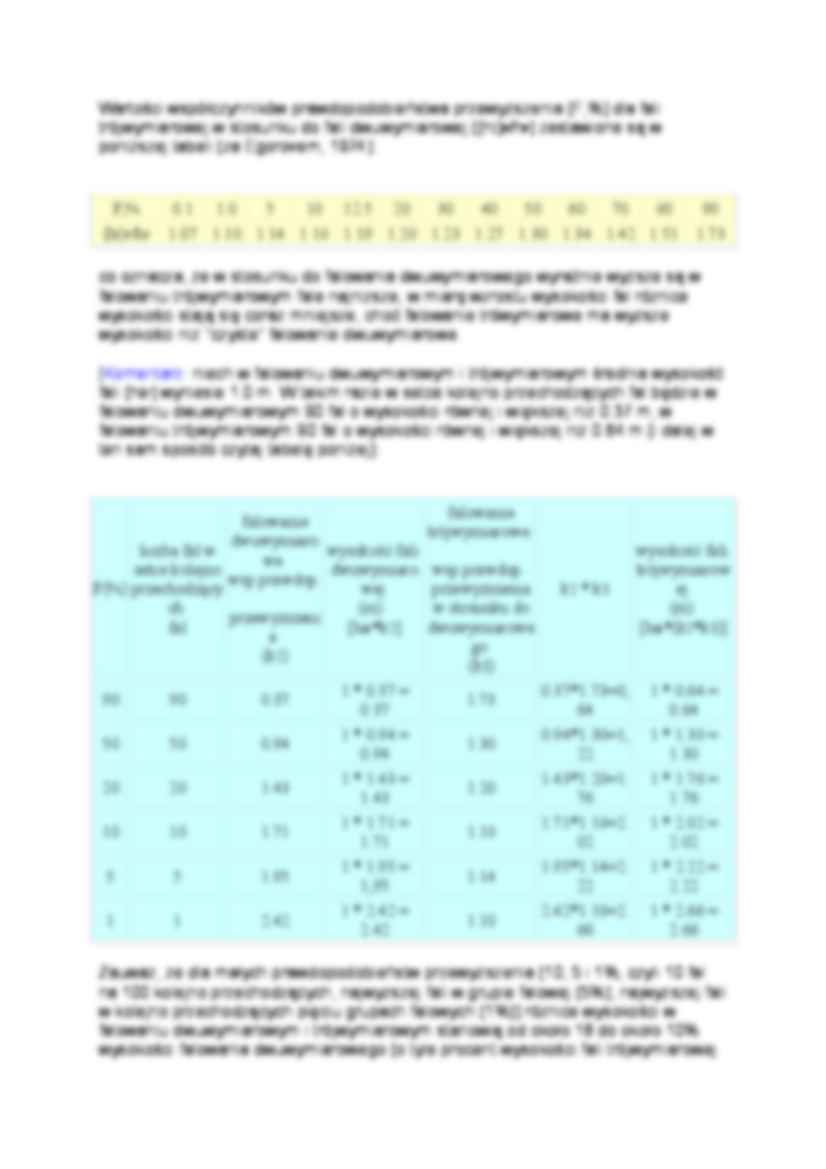

Falowanie trówymiarowe Występujące na morzu falowanie tylko w wyjątkowych wypadkach stanowi jednorodne falowanie wiatrowe lub falowanie rozkołysu. Z reguły na występujące falowanie wiatrowe nakłada się falowanie rozkołysu nadchodzące z bliższych lub dalszych odległości. Podobnie na jeden system rozkołysu nakładać się może inny system rozkołysu. W przypadku falowania wiatrowego i zmiany kierunku wiatru w czasie jego generowania, na stary system falowania, który może się jeszcze aktywnie rozwijać, nakłada się już nowy system falowania. Nawet bez zmiany Występujące systemy falowania interferują ze sobą, tworząc falowanie trójwymiarowe. Interferujących jednocześnie ze sobą systemów falowania może być w polu falowania wiele znacznie więcej niż dwa. Cechą charakterystyczną falowania trówymiarowego jest to, że zatraca się linijna wyrazistość linii grzbietów i dolin fal. Grzbiety fal są stosunkowo krótkie i o nierównej wysokości. Patrząc na grzbiety fal zauważa się występowanie wyraźnie wyższych ich fragmentów, tworzących często wyraźne "góry" wody, znacznie wyższe niż pozostałe partie grzbietów. Wzdłuż linii dolin widoczne są w powierzchni morza wyraźne (lub mniej wyraźne) "zagłębienia bezodpływowe" - obniżenia powierzchni otoczone ze wszystkich stron wyżej położoną powierzchnią wody. Wysokości fali trójwymiarowej określają praktycznie dwa najwyższe systemy falowania. Znając wysokości średnie lub wysokości o odpowiednim współczynniku przewyższenia dwu podstawowych systemów falowania, można obliczyć wysokość fali trójwymiarowej za pomocą formuły: ht = [(hw * hw) + (hm * hm)] ^ (1/2), gdzie: ht - wysokość fali trówymiarowej, hw - wysokość fali wiatrowej (pierweszego systemu falowania), hm - wysokość fali martwej; rozkołysu (drugiego systemu falowania). [Uwaga do wzoru: ht jest pierwiastkiem z sumy kwadratów wysokości obu systemów falowania]. Przykładowo; niech falowanie trówymiarowe powstaje z dwu systemów falowania: wiatrowego o wysokości średniej; hw = 2.0 m i falowania rozkołysu o średniej wysokości hm = 1.5 m. Wtedy wysokość średnia falowania trójwymiarowego będzie wynosić: (2.0 ^2) + (1.5 ^2) = 4 + 2.25 = 6.25; 6.25 ^ 0.5 = 2.5 m. W przypadku, gdy wysokość wiatrowej fali znacznej będzie wynosić będzie 4.0 m a nakładający się na nią system rozkołysu będzie miał również wysokość 4.0 m (wysokość fali znacznej), wysokość fali znacznej systemu falowania trójwymiarowego będzie: (4^2) + (4^2) = 16 + 16 = 32; 32^(1/2) = 5.66 = ~5.7 m.
(…)
….
Niech odczytana z mapy falowania kombinowanego (a więc bez wątpienia
falowania trójwymiarowego) wysokość fali znacznej (h1/3) wyniesie 8.0 m, a więc fala
jest bardzo wysoka (stan morza VII). Średnia wysokość falowania dwuwymiarowego
wyniesie wtedy: 8/1.61 = 4.97 m; zaokrąglamy do 5 m. Średnia wysokość fali
znacznej trójwymiarowej będzie wtedy 5 * (0.94 * 1.30) = 5 * (1.222) = ~5 * 1,22 = 6,1
m. Tu różnica…
... zobacz całą notatkę






Komentarze użytkowników (0)