To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Ćwiczenia 7 - 25 -
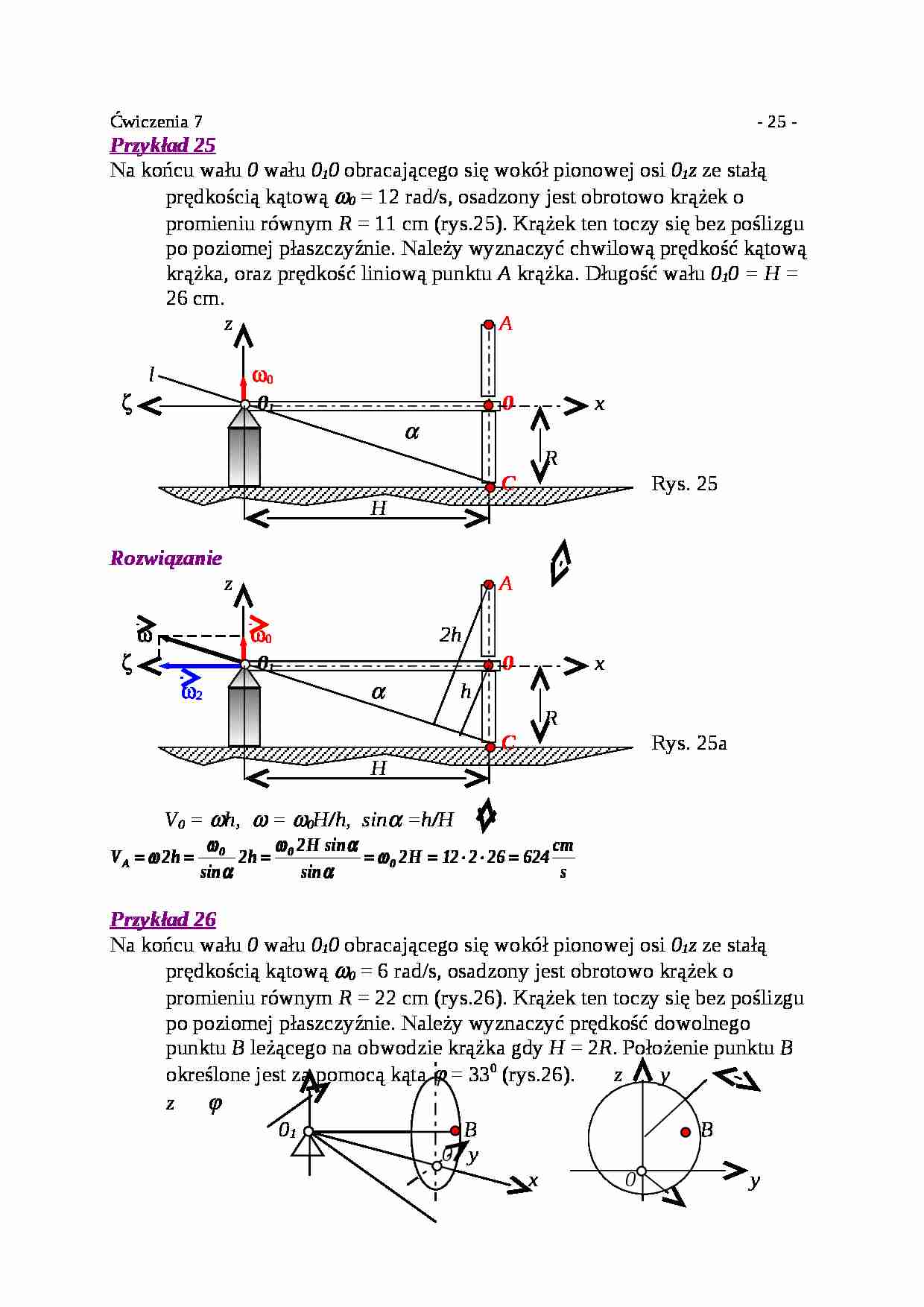
Przykład 25 Na końcu wału 0 wału 0 1 0 obracającego się wokół pionowej osi 0 1 z ze stałą prędkością kątową ω 0 = 12 rad/s, osadzony jest obrotowo krążek o promieniu równym R = 11 cm (rys.25). Krążek ten toczy się bez poślizgu po poziomej płaszczyźnie. Należy wyznaczyć chwilową prędkość kątową krążka, oraz prędkość liniową punktu A krążka. Długość wału 0 1 0 = H = 26 cm. z A l ω 0 ζ 0 1 0 x α R C Rys. 25 H Rozwiązanie z A ω ω 0 2h ζ 0 1 0 x ω 2 α h R C Rys. 25a H V 0 = ω h, ω = ω 0 H/h, sin α =h/H Przykład 26 Na końcu wału 0 wału 0 1 0 obracającego się wokół pionowej osi 0 1 z ze stałą prędkością kątową ω 0 = 6 rad/s, osadzony jest obrotowo krążek o promieniu równym R = 22 cm (rys.26). Krążek ten toczy się bez poślizgu po poziomej płaszczyźnie. Należy wyznaczyć prędkość dowolnego punktu B leżącego na obwodzie krążka gdy H = 2 R . Położenie punktu B określone jest za pomocą kąta ϕ = 33 0 (rys.26). z y z ϕ 0 1 B B 0 y x 0 y
(…)
… = 30 rad/s (rys.27). Krążek toczy się bez poślizgu po poziomej płaszczyźnie. Promień krążka R = 21 cm, H = 35 cm.
z A
l ω0 ζ 01 0 x
α R
C Rys. 27
H
Rozwiązanie - 27 -
z A
rA ω ω0 h
ζ 01 0 x
ω2 α rC R
C Rys. 27a
H
y
ω2 01 x
ε ε Ponieważ jest to precesja regularna to ω1 = ω0 Z wzoru (79)wykład 7 strona 50, lub Jan Misiak
tom II strona 113, wzór (24.26)
(a)
z (a) Przyśpieszenie punktu C z wzoru (82) (patrz wykład 7)
, ponieważ , to z A
01 0 x
aC jest prostopadle do osi obrotu 01C, ε rC 900 aC
a zwrot pokazano na rysunku 27b. 01 rC C
Rys. 27b ε 900 aC
Przyśpieszenie punktu A - 28 -
a1A rA 01a1A
ε 900 A
z rA 01 0 x
Rys. 27c
ω z VA
a2A = 2a1A a2A
01 0 x
900 Rys. 27d C
2α a1A
aA A
z 900 a2A
01 2α x
900 C Rys. 27e
Z rys. 27e
…
... zobacz całą notatkę






Komentarze użytkowników (0)