To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Wykład 6
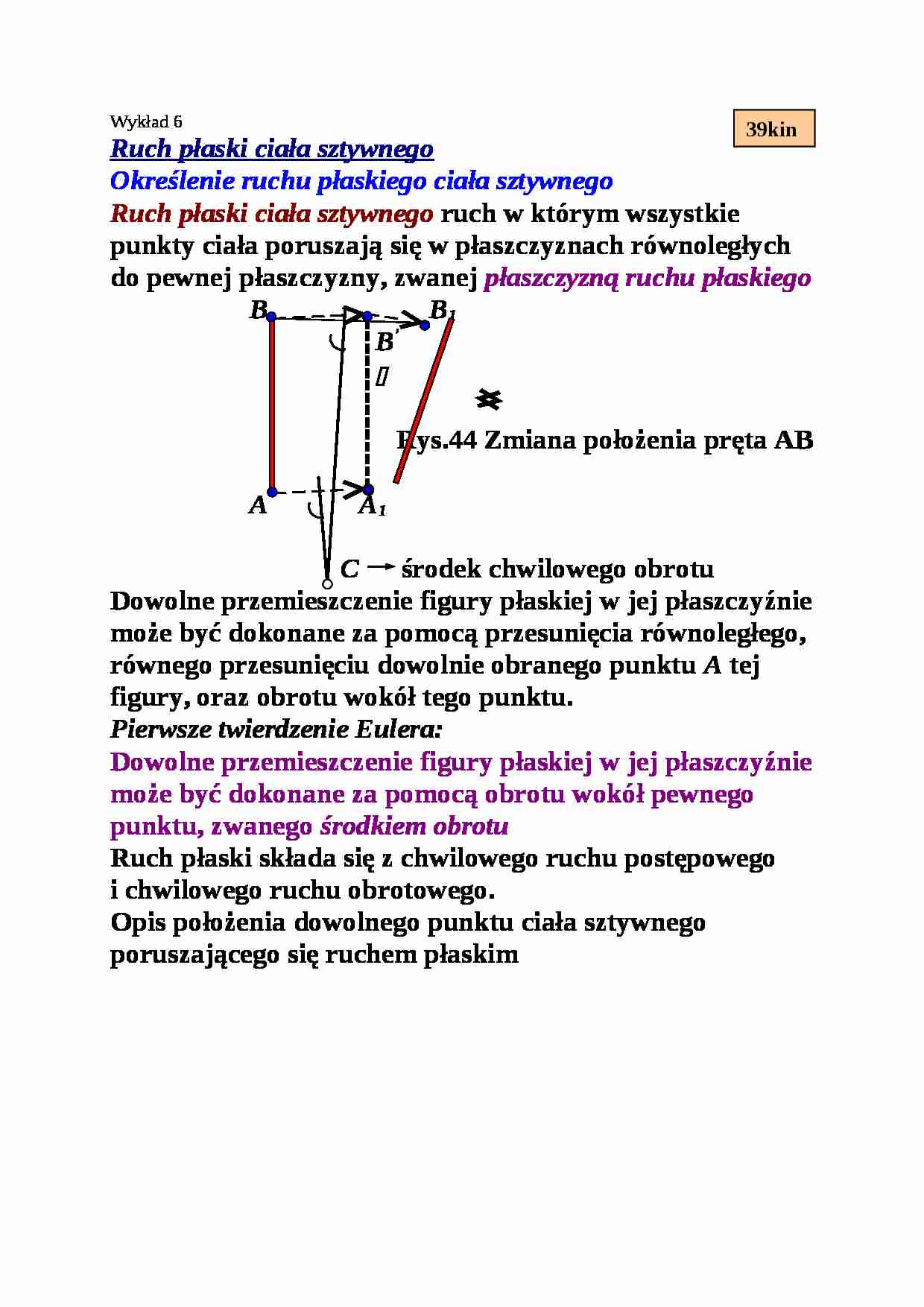
Ruch płaski ciała sztywnego Określenie ruchu płaskiego ciała sztywnego Ruch płaski ciała sztywnego ruch w którym wszystkie punkty ciała poruszają się w płaszczyznach równoległych do pewnej płaszczyzny, zwanej płaszczyzną ruchu płaskiego B B 1 B ' * Rys.44 Zmiana położenia pręta AB A A 1 C środek chwilowego obrotu Dowolne przemieszczenie figury płaskiej w jej płaszczyźnie może być dokonane za pomocą przesunięcia równoległego, równego przesunięciu dowolnie obranego punktu A tej figury, oraz obrotu wokół tego punktu. Pierwsze twierdzenie Eulera: Dowolne przemieszczenie figury płaskiej w jej płaszczyźnie może być dokonane za pomocą obrotu wokół pewnego punktu, zwanego środkiem obrotu Ruch płaski składa się z chwilowego ruchu postępowego i chwilowego ruchu obrotowego. Opis położenia dowolnego punktu ciała sztywnego poruszającego się ruchem płaskim Y y Y B B * x r B r * Y A A 0 X A X B X r A ω Z z ε Rys.45 Ruch dowolne go punktu B figury płaskiej w układzie nieruchomym opisujemy za pomocą promienia wektora r B r B = r A + r Prędkość punktu B (a) Ponieważ wektor r nie zmienia długości, zmienia tylko kierunek obracając się z prędkością kątową i przyśpieszeniem kątowym , stąd podstawiając to do (a) otrzymujemy (b) gdzie r x = X B - X A , r y = Y B - Y A , r z = Z B - Z A stąd składowe prędkości w układzie nieruchomym są:
(…)
…
Składowe prędkości punktu B w układzie 0XYZ
Różniczkując (c) względem czasu (63)
Przykład 15
Na rys.49 przedstawiony jest schematycznie mechanizm korbowy silnika samochodu, składający się: z wału korbowego OA, który obraca się wokół osi 0, korbowodu AB, oraz tłoka B. Końce korbowodu połączone są przegubowo z tłokiem i wałem. Należy wyznaczyć prędkość tłoka jeśli wał obraca się ze stałą prędkością ω. Długość wykorbienia równa jest r, a długość korbowodu l.
Y A y
r α l = x
h * B
X
0 XB
x
Rys.49 α = ωt
Rozwiązanie
; ; dla , niech: n = 3600obr/min, k = 0.1, r = 2.5cm, wtedy Metoda chwilowego środka obrotu
β
B VB
VA α
A ω (64)
0
Rys.50 0 środek chwilowego obrotu ciała AB Przykład 16
Dla konstrukcji i danych z przykładu 15 określić prędkość tłoka metodą środka chwilowego obrotu.
C
ω1
VA = ωr
900
A l 900
ω…
... zobacz całą notatkę






Komentarze użytkowników (0)