To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Ćwiczenia 6 - 24 -
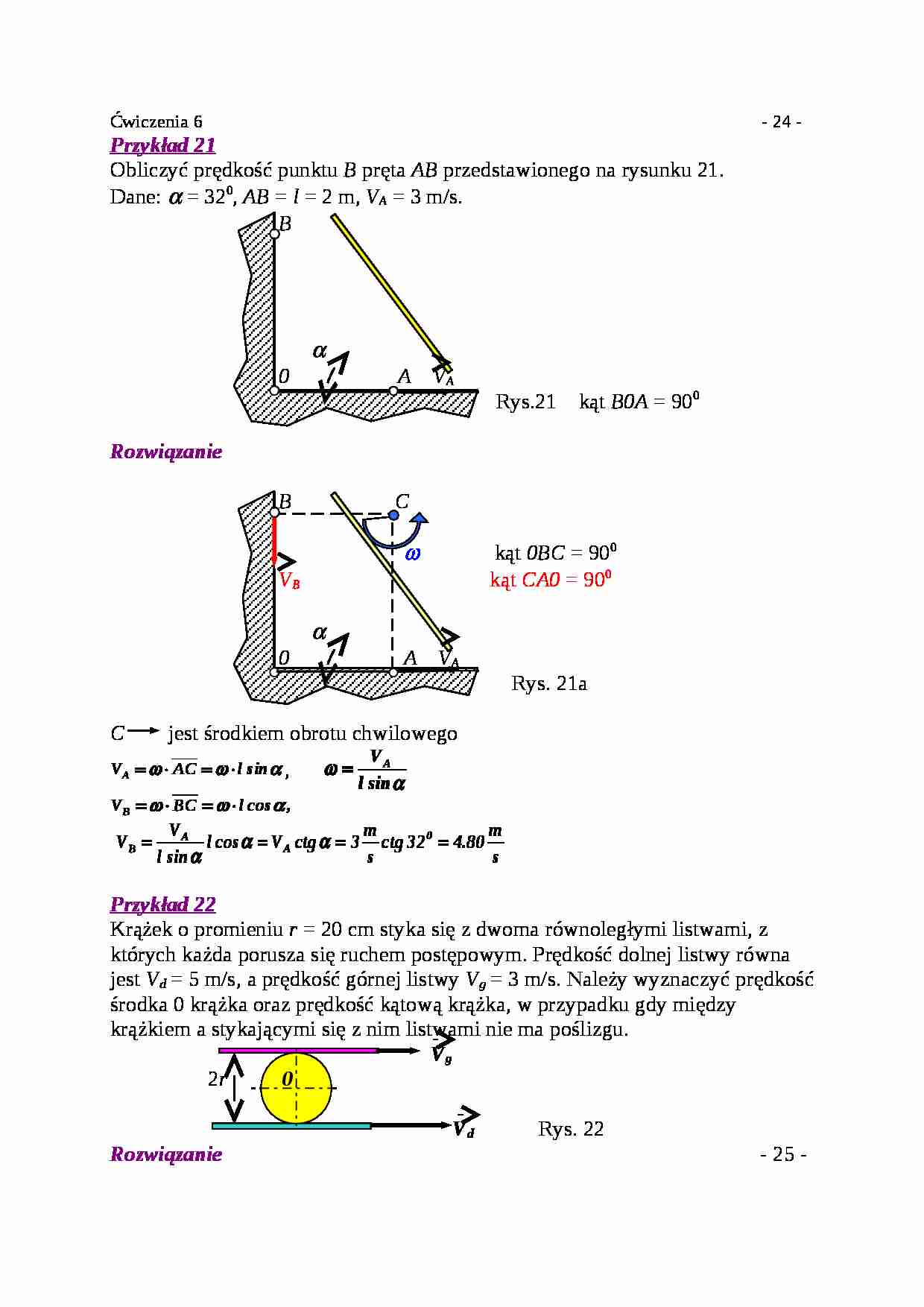
Przykład 21 Obliczyć prędkość punktu B pręta AB przedstawionego na rysunku 21.
Dane: α = 32 0 , AB = l = 2 m, V A = 3 m/s. B α 0 A V A Rys.21 kąt B0A = 90 0 Rozwiązanie B C ω kąt 0BC = 90 0 V B kąt CA0 = 90 0 α 0 A V A Rys. 21a C jest środkiem obrotu chwilowego
, Przykład 22 Krążek o promieniu r = 20 cm styka się z dwoma równoległymi listwami, z których każda porusza się ruchem postępowym. Prędkość dolnej listwy równa jest V d = 5 m/s, a prędkość górnej listwy V g = 3 m/s. Należy wyznaczyć prędkość środka 0 krążka oraz prędkość kątową krążka, w przypadku gdy między krążkiem a stykającymi się z nim listwami nie ma poślizgu.
V g 2 r 0 V d Rys. 22
Rozwiązanie - 25 - V g V g ω V g ω V 0 ω r V d V g ω r r V d ω V d V d Rys. 22a Rys. 22b Rys. 22c
(…)
… wyznaczamy środek chwilowego obrotu 0, który leży w punkcie przecięcia się tych prostopadłych>
Ponieważ kąt 0AB = 600, a kąt 0BA = 300, przeto trójkąt AB0 jest trójkątem prostokątnym. Dlatego:
, Prędkość kątowa odcinka AB
(a)
Wartość liczbowa punktu B
(b)
Aby wyznaczyć wartość liczbową prędkości punktu C, należy określić długość promienia 0C. Ponieważ kąt 0AB = 600, a , dlatego trójkąt 0AC jest trójkątem równobocznym. Mamy więc:
(c)
Prędkość VC jako prostopadła do promienia 0C, jest nachylona pod kątem 300 do odcinka AB.
Podstawiając do wzorów (a), (b) i (c) l = 0.5 m, VA = 10 m/s, otrzymujemy: , VB =17.3 m/s, VC = 10 m/s.
…
... zobacz całą notatkę






Komentarze użytkowników (0)