Belka ukośna

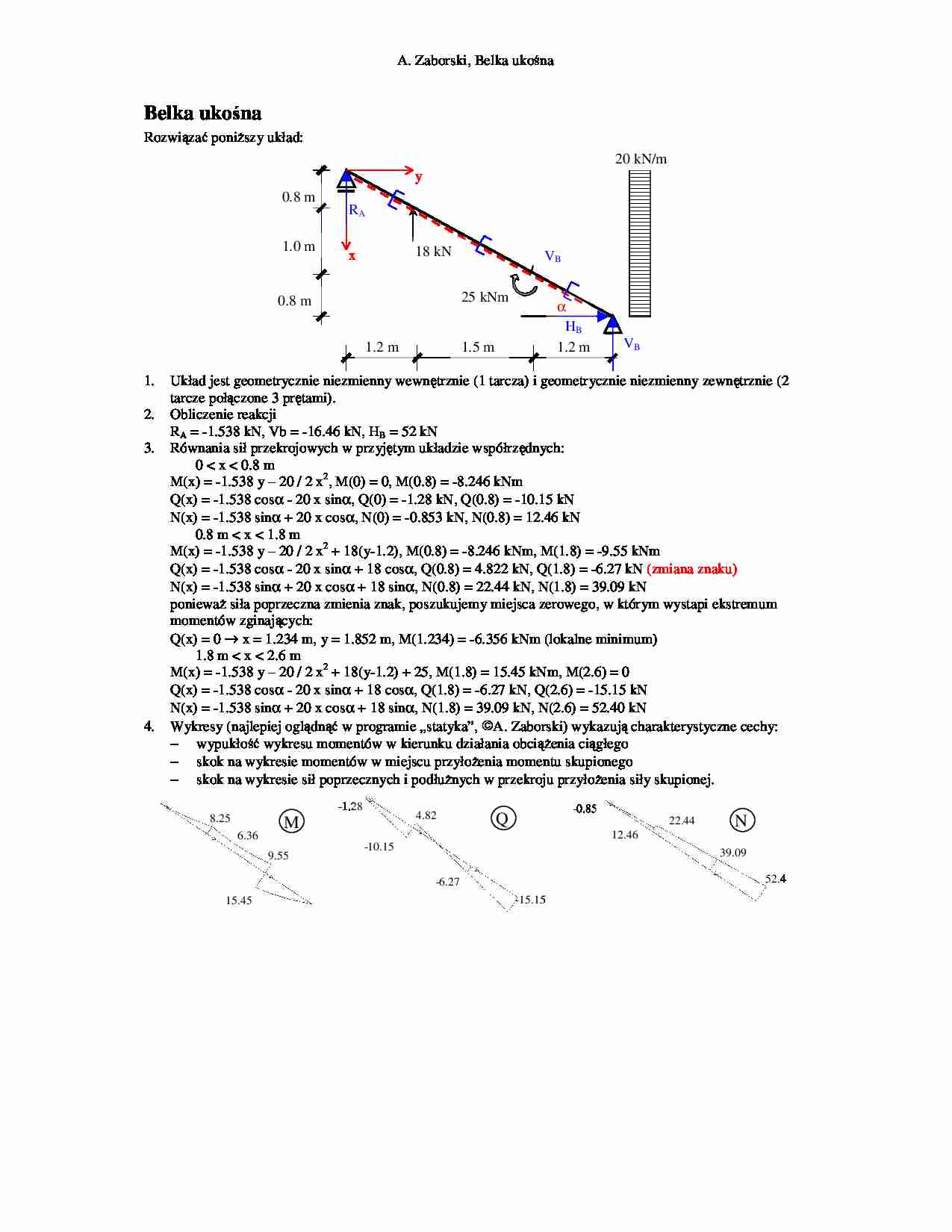
A. Zaborski, Belka uko na  Belka uko na  Rozwi za  poni szy układ:  VB RA 1.0 m 0.8 m 0.8 m 1.5 m 1.2 m 1.2 m α y x 18 kN 25 kNm 20 kN/m VB HB   1.  Układ jest geometrycznie niezmienny wewn trznie (1 tarcza) i geometrycznie niezmienny zewn trznie (2  tarcze poł czone 3 pr tami).  2.  Obliczenie reakcji  RA = -1.538 kN, Vb = -16.46 kN, HB = 52 kN  3.  Równania sił przekrojowych w przyj tym układzie współrz dnych:  0 

(…)

… znaku)
N(x) = -1.538 sinα + 20 x cosα + 18 sinα, N(0.8) = 22.44 kN, N(1.8) = 39.09 kN
poniewa siła poprzeczna zmienia znak, poszukujemy miejsca zerowego, w którym wystapi ekstremum
momentów zginaj cych:
Q(x) = 0 → x = 1.234 m, y = 1.852 m, M(1.234) = -6.356 kNm (lokalne minimum)
1.8 m < x < 2.6 m
M(x) = -1.538 y – 20 / 2 x2 + 18(y-1.2) + 25, M(1.8) = 15.45 kNm, M(2.6) = 0
Q(x) = -1.538 cosα - 20 x sinα + 18 cosα, Q(1.8) = -6.27 kN, Q(2.6) = -15.15 kN
N(x) = -1.538 sinα + 20 x cosα + 18 sinα, N(1.8) = 39.09 kN, N(2.6) = 52.40 kN
4. Wykresy (najlepiej ogl dn w programie „statyka”, A. Zaborski) wykazuj charakterystyczne cechy:
− wypukło wykresu momentów w kierunku działania obci enia ci głego
− skok na wykresie momentów w miejscu przyło enia momentu skupionego
− skok na wykresie sił poprzecznych…
... zobacz całą notatkę