To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
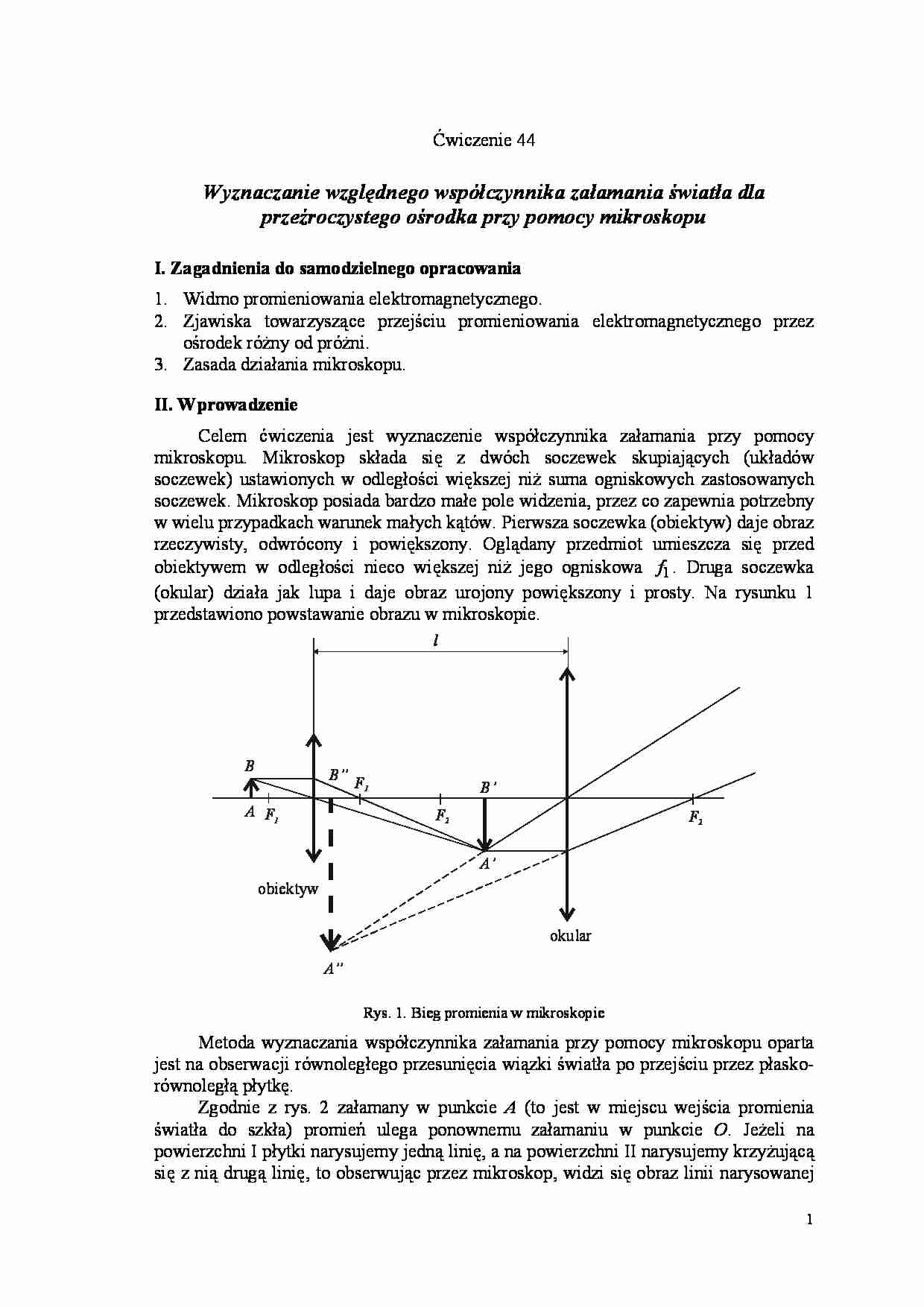


1 Ćwiczenie 44 Wyznaczanie względnego współczynnika załamania światła dla przeźroczystego ośrodka przy pomocy mikroskopu I. Zagadnienia do samodzielnego opracowania 1. Widmo promieniowania elektromagnetycznego. 2. Zjawiska towarzyszące przejściu promieniowania elektromagnetycznego przez ośrodek różny od próżni. 3. Zasada działania mikroskopu. II. Wprowadzenie Celem ćwiczenia jest wyznaczenie współczynnika załamania przy pomocy mikroskopu. Mikroskop składa się z dwóch soczewek skupiających (układów soczewek) ustawionych w odległości większej niż suma ogniskowych zastosowanych soczewek. Mikroskop posiada bardzo małe pole widzenia, przez co zapewnia potrzebny w wielu przypadkach warunek małych kątów. Pierwsza soczewka (obiektyw) daje obraz rzeczywisty, odwrócony i powiększony. Oglądany przedmiot umieszcza się przed obiektywem w odległości nieco większej niż jego ogniskowa 1 f . Druga soczewka (okular) działa jak lupa i daje obraz urojony powiększony i prosty. Na rysunku 1 przedstawiono powstawanie obrazu w mikroskopie. okular obiektyw A A’ A’ B’’ B’ B F 1 F 1 F 2 F 2 l Rys. 1. Bieg promienia w mikroskopie Metoda wyznaczania współczynnika załamania przy pomocy mikroskopu oparta jest na obserwacji równoległego przesunięcia wiązki światła po przejściu przez płasko- równoległą płytkę. Zgodnie z rys. 2 załamany w punkcie A (to jest w miejscu wejścia promienia światła do szkła) promień ulega ponownemu załamaniu w punkcie O . Jeżeli na powierzchni I płytki narysujemy jedną linię, a na powierzchni II narysujemy krzyżującą się z nią drugą linię, to obserwując przez mikroskop, widzi się obraz linii narysowanej 2 na powierzchni II nie w punkcie O , lecz w miejscu oznaczonym na rysunku O' . Oznaczamy grubość płytki przez " OO d = zaś grubość pozorną " ' ' O O d = . Z trygonometrycznych zależności wynika: α tg ' " = d AO , β tg " = d AO skąd: α β tg tg ' d d = (1a) d d’ A O O’ O’’ α α β β Rys. 2. Bieg promienia przez płasko-równoległą płytkę Dla niewielkich kątów padania i załamania można przyjąć: w n d d d = = α β sin sin ' (1b) gdzie w n względny współczynnik załamania szkła. Zatem: ' d d nw = III. Wykonanie ćwiczenia 1. Przygotować mikroskop do pomiarów ustawiając równo oświetlone pole widzenia. 2. Otrzymane dwie płytki płasko-równoległe o różnych grubościach starannie oczyścić. 3. Śrubą mikrometryczną zmierzyć grubość płytek
(…)
…
pionowego aż do zauważenia minimalnej zmiany ostrości obrazu. Dokonać pomiaru i
obliczyć odległość ∆ d '1 , o jaką zmienia się położenie obiektywu. Podobnie oszacować
∆ d '2 , tj. zmianę położenia układu optycznego w kierunku przeciwnym wywołującą
zauważalną zmianę ostrości obrazu.
∆ d '1 + ∆ d '2
∆d ' =
2
Błędy współczynnika załamania ∆ n1 i ∆ n2 obliczyć wykorzystując metodę
różniczki zupełnej…
... zobacz całą notatkę






Komentarze użytkowników (0)