To tylko jedna z 8 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
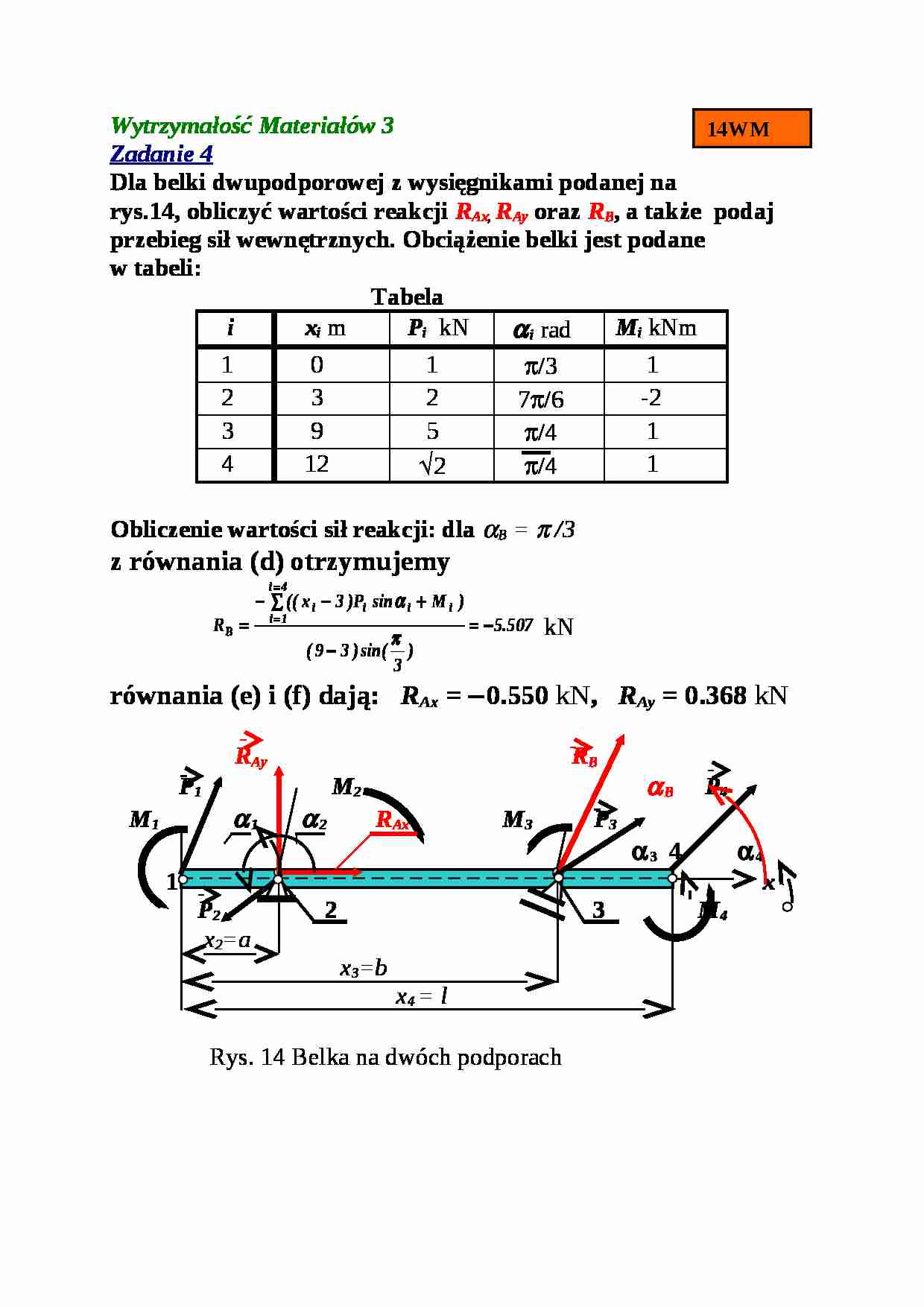

Wytrzymałość Materiałów 3 Zadanie 4 Dla belki dwupodporowej z wysięgnikami podanej na rys.14, obliczyć wartości reakcji R Ax , R Ay oraz R B , a także podaj przebieg sił wewnętrznych. Obciążenie belki jest podane w tabeli: Tabela i x i m P i kN α i rad M i kNm 1
0
1
π/3
1
2
3
2
7π/6
-2 3
9
5
π/4
1
4
12
√2
π/4
1
Obliczenie wartości sił rea kcji: dla α B = π /3 z równania (d) otrzymujemy kN
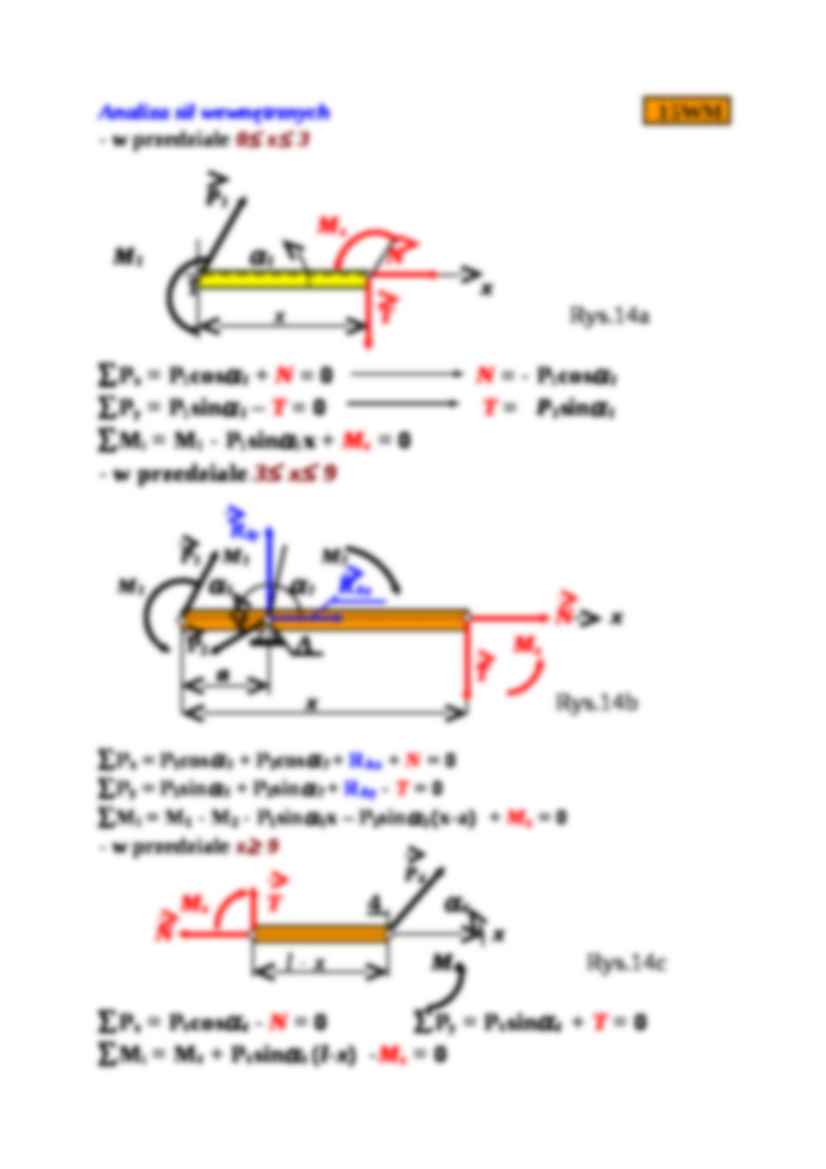
równania (e) i (f) dają: R Ax = − 0.550 kN , R Ay = 0.368 kN R Ay R B P 1 M 2 α B P 4 M 1 α 1 α 2 R Ax M 3 P 3 α 3 4 α 4 1 x P 2 2 3 M 4 x 2 =a x 3 =b x 4 = l Rys. 14 Belka na dwóch podporach Analiza sił wewnętrznych 15WM - w przedziale 0 ≤ x ≤ 3 P 1 M x M 1 α 1 N 1 x x T Rys.14a ∑ P x = P 1 cos α 1 + N = 0 N = - P 1 cos α 1 ∑ P y = P 1 sin α 1 - T = 0 T = P 1 sin α 1 ∑ M i = M 1 - P 1 sin
(…)
… zginaniu
P a A B a P
RA RB Mg=Pa T=P T = 0
T = P Rys. 15 Realizacja czystego zginania O 17WM
ρ - ro d* z
ρ ρ -z s
A B A B
s1 z z2 s x x
D C z1
D C
Rys. 13 Określenie odkształceń względnych s = ρd*, s1 = (ρ - z)d* (7) Z prawa Hooke'a mamy: * = Eε = -Ez ρ (8)
x
z
M = My
Mz = 0
T = 0
z2 N = 0
z x
y
- z1
My y
Rys.17 y oś obojętna, * = 0
Rys.17a, obraz rzeczywistego stanu naprężeń Rys.17a
Określenie położenia osi obojętnej 18WM
1) z warunku N = 0
wniosek oś y (oś obojętna) jest osią przechodzącą przez środek ciężkości taka oś nazywa się
osią centralną takich osi jest nieskończona ilość
2) MZ = 0
odśrodkowy moment bezwładności
Jeśli Jyz = 0 to osie y,z nazywamy osiami głównymi,
jeśli te osie przechodzą przez środek ciężkości przekroju to nazywamy je osiami głównymi centralnymi.
3) My = Mg (8a)
mnożymy…
… przekroju kołowego.
Wyprowadzenie wzoru.
z dF = dsdr = rd*dr
* z=rsin*
x
dr Rys.16
(10) z wzoru (9) mamy : (10a) gdzie wskaźnik wytrzymałości
dla przekroju kołowego pełnego Z wzoru (10a) i warunku że *max = *e = 75MPa mamy:
Linia ugięcia belki 20WM
Z wzoru (8a) mamy 1 ρ = Mg(x) EJy w(x) ρ P
ϑ
A x
x wx l
Rys.16 Określenie ugięć belki (w przekroju A belka zamurowana)
Z geometrii różniczkowej wiemy…
... zobacz całą notatkę






Komentarze użytkowników (0)