To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

5. Analiza stanu naprę enia i odkształcenia
5. ANALIZA STANU NAPRĘ ENIA I ODKSZTAŁCENIA
5.1. Analiza płaskiego stanu naprę enia
Płaski stan naprę enia - na myślowo
wyciętą, elementarną kostkę działają
naprę enia w jednej płaszczyźnie (1-2)
2
σ2
2
1, 2 – osie główne
σ1, σ2 – naprę enia
główne
(brak naprę eń
stycznych)
1
σ2
σ1
1
σ1
σ1
3
σ1
σ2
σ2
σ2
2
σ2
2
σα
σ1
τα
σ'α
α
1
σ1
2
σ" α
α
τ'α
1
τ"α
σ2
α
1
σ2
'
"
σα = σα + σα
'
σ α = σ 1 cos 2 α
'
"
τα = τα + τα
'
τ α = σ 1 sin α cosα
σα =
σ1 + σ 2 σ1 −σ2
2
τα =
+
σ1 −σ2
2
- 1/6 -
2
"
σ α = σ 2 sin 2 α
"
τ α = −σ 2 sin α cosα
cos 2α
sin 2α
5. Analiza stanu naprę enia i odkształcenia
Koło Mohra dla naprę eń
Zadanie: Dane są naprę enia główne σ1, σ2. Znaleźć naprę enia na ściankach kostki
obróconej o kąt α.
2
τ
σ2
τα
σα+π/2
τα+π/2
2 α +π
2α
σα+π/2
σ2
σ
σ1
σ1
σα
α
τα
σα
1
σ1
τα+π/2
σ2
(σ1+σ2)/2
Kolejność postępowania:
1. rysujemy układ współrzędnych σ,τ ,
2. na osi poziomej zaznaczamy naprę enia σ1 i σ2 ,
3. ze środka (σ1+σ2)/2 rysujemy okrąg przechodzący przez punkty σ1 i σ2 ,
4. poziomą średnicę koła obracamy o kąt 2α ,
5. odczytujemy naprę enia
− dla krawędzi nachylonej pod kątem α : σα, τα ,
− dla krawędzi prostopadłej : σα+π/2, τα+π/2 .
Zadanie odwrotne: Na ściankach kostki dane są naprę enia σx, σy, τ. Znaleźć
poło enie osi głównych i naprę enia główne.
y
σy
τ
τ
τ
2
τx
σ2
σ1
σx
σx
σ1
σ2
σy
τ
σ2
x
σy
2α
σx
τ α
1
-τ
- 2/6 -
σ1
σ
5. Analiza stanu naprę enia i odkształcenia
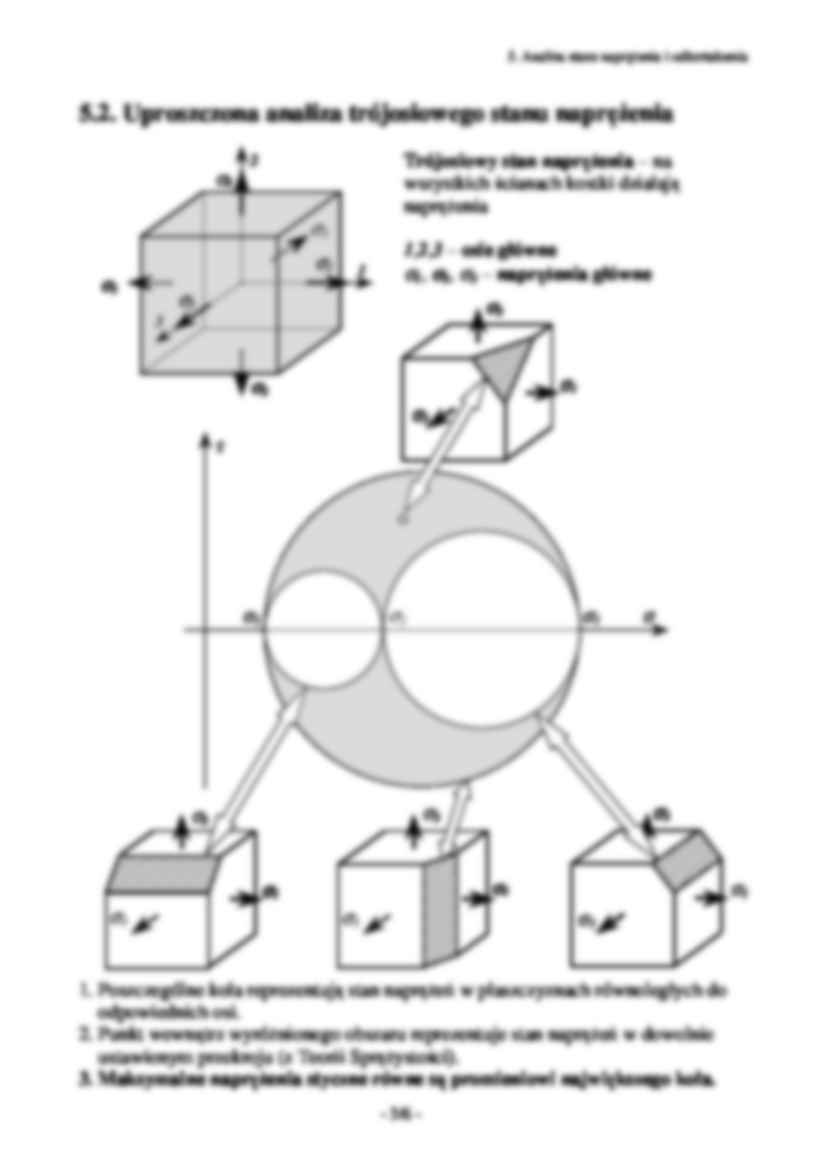
5.2. Uproszczona analiza trójosiowego stanu naprę enia
Trójosiowy stan naprę enia – na
wszystkich ścianach kostki działają
naprę enia
2
σ2
σ3
σ1
σ1
1
1,2,3 – osie główne
σ1, σ2, σ3 – naprę enia główne
σ3
σ2
3
σ1
σ2
σ3
τ
σ3
σ2
σ
σ2
σ2
σ2
σ1
σ1
σ3
σ1
σ3
σ1
σ3
1. Poszczególne koła reprezentują stan naprę eń w płaszczyznach równoległych do
odpowiednich osi.
2. Punkt wewnątrz wyró nionego obszaru reprezentuje stan naprę eń w dowolnie
ustawionym przekroju (z Teorii Sprę ystości).
3. Maksymalne naprę enia styczne równe są promieniowi największego koła.
- 3/6 -
5. Analiza stanu naprę enia i odkształcenia
5.3. Uproszczona analiza stanu odkształcenia
2
α
ε2
1
Elementarna myślowo wycięta kostka, znajdująca
się w płaskim stanie odkształcenia, doznaje
wydłu eń względnych jak na rysunku:
− na kierunku 1: ε1
− na kierunku 2: ε2
Na kierunku nachylonym pod kątem α
odkształcenia kostki wyniosą:
− wydłu enie względne
ε α = ε 1 cos 2 α + ε 2 sin 2 α
ε1
− kąt odkształcenia postaciowego
1,2 – główne osie odkształcenia
ε1, ε2 – odkształcenia główne
γ α = 2(ε1 − ε 2 )sin α cosα
(patrz: Analiza stanu odkształcenia rozciąganego pręta)
Koło Mohra dla płaskiego stanu odkształcenia
γ/2
γα/2
2 α +π
ε2
εα+π/2
2α
ε1
ε
εα
γα+π/2/2
(ε1+ε2)/2
Kolejność postępowania:
1. rysujemy układ współrzędnych ε,γ/2,
2. na osi poziomej zaznaczamy wydłu enia ε1 i ε2 ,
3. ze środka (ε1+ε2)/2 rysujemy okrąg przechodzący przez punkty ε1 i ε2 ,
4. poziomą średnicę koła
(…)
… stan odkształcenia w płaszczyznach
równoległych do odpowiednich osi.
2. Punkt wewnątrz wyró nionego obszaru reprezentuje stan odkształcenia w
dowolnie ustawionym przekroju (z Teorii Sprę ystości).
3. Maksymalny kąt odkształcenia postaciowego równy jest średnicy
największego koła.
4. W ka dym stanie odkształcenia istnieją tylko 3 kierunki główne (1, 2, 3), między
którymi pierwotne kąty proste…
... zobacz całą notatkę






Komentarze użytkowników (0)