To tylko jedna z 13 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
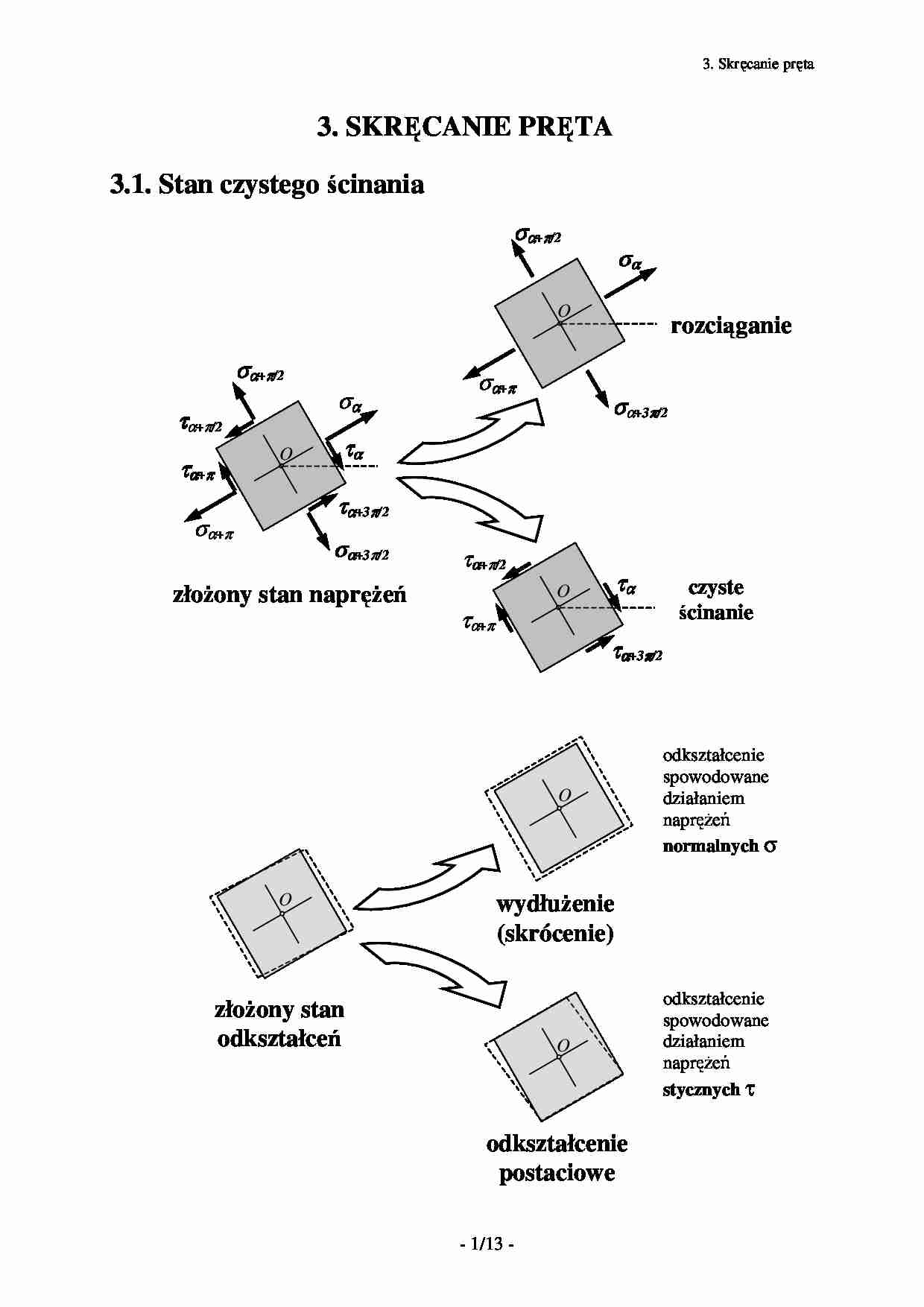


3. Skręcanie pręta
3. SKRĘCANIE PRĘTA
3.1. Stan czystego ścinania
σα+π/2
σα
O
σα+π/2
σα
τα+π/2
O
τα+π
rozciąganie
σα+π
σα+3π/2
τα
τα+3π/2
σα+π
σα+3π/2
τα+π/2
zło ony stan naprę eń
τα
O
τα+π
czyste
ścinanie
τα+3π/2
O
O
odkształcenie
spowodowane
działaniem
naprę eń
normalnych σ
wydłu enie
(skrócenie)
zło ony stan
odkształceń
O
odkształcenie
postaciowe
- 1/13 -
odkształcenie
spowodowane
działaniem
naprę eń
stycznych τ
3. Skręcanie pręta
∆a
B’
τ
B
kąt odkształcenia postaciowego
γ
A’
A
τ = σ 0 sin α cos α
TAB
γ=
τ
2(1 + ν )
σ 0 sin α cos α
E
γ=
2(1 + ν )
τ=
E
a
τ
b
C
D
τ
E
2(1 + ν )
τ
E
=G
2(1 + ν )
moduł sztywności
postaciowej
(moduł Kirchhoffa)
γ=
τ
G
prawo Hooke’a
przy ścinaniu
5
dla stali: E≈2.1⋅105MPa, ν≈0.3 ⇒ G≈0.81⋅10 MPa
≈
⋅
5
przykład: τ=200MPa, G≈0.81⋅10 MPa ⇒ γ=2.47⋅10-3rad=0.14o≈8.5’
3.2. Energia wewnętrzna w stanie czystego ścinania
TAB = bh ⋅ τ
- wypadkowa siła działająca na brzegu AB (h – grubość kostki)
Energia wewnętrzna U zgromadzona w kostce równa jest pracy siły TAB na
przemieszczeniu ∆a=γa
1
1
U = TAB ∆a = bhτγa [ J ]
2
2
Energia wewnętrzna na jednostkę objętości
U
1
τ 2 γ 2G
Uv =
= τγ =
=
[ J / m3 ]
abh 2
2G
2
- 2/13 -
3. Skręcanie pręta
3.3. Skręcanie rury cienkościennej
realizacja stanu czystego ścinania
Ms
z
Ms
τ
y
O
Ms
elementarna
kostka
x
τ
dF=τδ Rdβ
dβ
R
2π
β
Ms =
O
2π
∫ RdF = ∫ τδR
0
δ
2
dβ = 2πτδ R 2
0
τ=
Ms
2πδ R2
stan czystego
ścinania
τ
γ
τ
τ
τ
elementarna kostka
wycięta ze ścianki rury
z
Ms
γ
Ms
ilustracja kąta odkształcenia postaciowego
na powierzchni skręcanej rury
- 3/13 -
x
3. Skręcanie pręta
τ
τe
τp
granica plastyczności przy skręcaniu
granica proporcjonalności
(granica stosowalności prawa
Hooke’a) przy skręcaniu
Przykładowy wykres skręcania
Próbka do statycznej próby skręcania
(Zb.Brzoska, Wytrzymałość Materiałów, PWN Warszawa, 1979)
- 4/13 -
γ
3. Skręcanie pręta
3.4. Skręcanie pręta o przekroju kołowym
Skręcanie – przypadek obcią enia konstrukcji, gdy w myślowym
przekroju istnieje moment skręcający Ms.
l
Ms
z
z
y
y
γ
ϕ
A
dw=2rw
dz=2rz
A’
x
x
przed obcią eniem
− na powierzchni pręta
narysowano prostokątną siatkę
o krawędziach równoległych do
osi pręta
Ms
po obcią eniu pręta momentem
skręcającym Ms
− siatka prostokątna zmienia się na
ukośnokątną
− łuki kół pozostają nie zmienione
− linie równoległe do osi zmieniają
się na linie śrubowe nachylone
pod kątem γ
− przekroje końcowe odcinka pręta
skręcają się względem siebie o
kąt ϕ
Hipoteza płaskich przekrojów:
Przy skręcaniu pręta kołowego przekroje poprzeczne nie doznają
adnych odkształceń, a jedynie obracają się wokół osi pręta.
- 5/13 -
3. Skręcanie pręta
Elementarna współśrodkowa rura o
promieniu r i grubości dr ulega skręceniu
o ten sam kąt ϕ, co i cały pręt.
z
ϕ
A’
τr
dr
A
B
r
B’
y
γr – kąt odkształcenia postaciowego
elementarnej rury
O
ϕr
BB' = γ r l = ϕr ⇒ γ r =
l
elementarna
współśrodkowa
rura
z prawa Hooke’a dla ścinania
τ r = Gγ
(…)
… PROFIL OTWARTY
Ws =
s1
δ1
δn
1
3δ max
n
∑
i =1
siδ i3
1 n
J s = ∑ siδ i3
3 i =1
sn
τmax
δi
– w środku dlugich boków odcinka
o grubości δmax
si
CIENKOŚCIENNA DOWOLNA RURA
n
Ws = 2 Fδ min
s1
δ1
F
δn
δi
sn
J s = 4F 2 ∑
si
i =1 δ i
τmax
– w miejscu, gdzie grubość ścianki jest
najmniejsza
si
F – pole ograniczone linią środkową
- 11/13 -
3. Skręcanie pręta
3.7. Naprę enia i odkształcenia sprę yny śrubowej
P
D…
… =
=
=
rmax
2
16
dla przekroju pełnego
wskaźnik wytrzymałości na skręcanie
3.5. Energia wewnętrzna w skręcanym pręcie
Jeśli zachowane jest prawo Hooke'a przy skręcaniu,
to energia wewnetrzna U zgromadzona w pręcie
równa jest pracy zewnętrznej wykonanej przez
moment skręcający Ms na przemieszczeniu ϕ
Ms
W
ϕ
1
M s2l
[J]
U = W = M sϕ =
2
2GJ 0
Energia wewnętrzna na jednostkę długości pręta
U
M s2
M Θ
Ul = =
= s…
... zobacz całą notatkę






Komentarze użytkowników (0)