To tylko jedna z 9 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


2. Rozciąganie (ściskanie) pręta
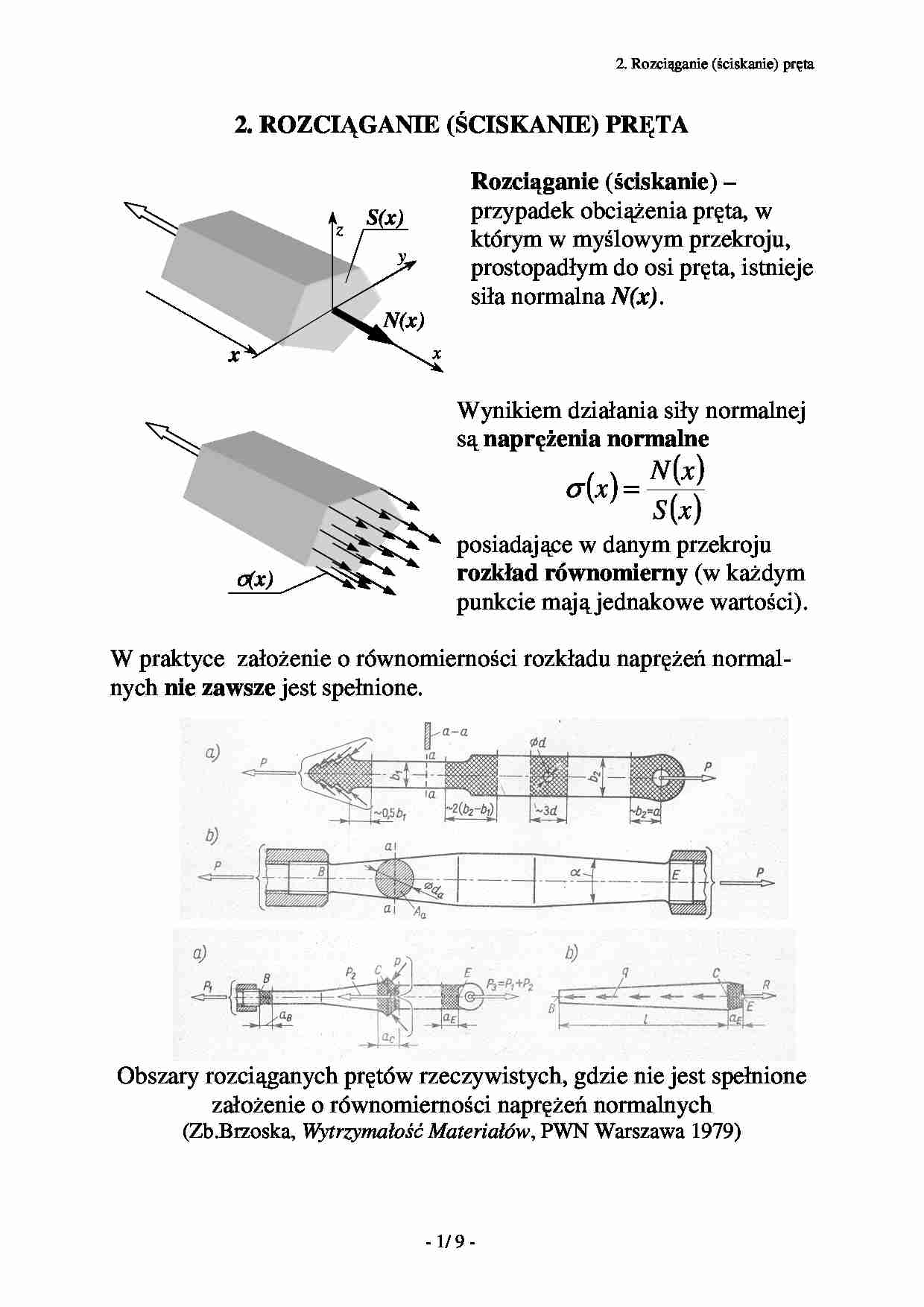
2. ROZCIĄGANIE (ŚCISKANIE) PRĘTA
z
Rozciąganie (ściskanie) –
przypadek obcią enia pręta, w
którym w myślowym przekroju,
prostopadłym do osi pręta, istnieje
siła normalna N(x).
S(x)
y
N(x)
x
x
Wynikiem działania siły normalnej
są naprę enia normalne
σ (x ) =
σ(x)
N (x )
S (x )
posiadające w danym przekroju
rozkład równomierny (w ka dym
punkcie mają jednakowe wartości).
W praktyce zało enie o równomierności rozkładu naprę eń normalnych nie zawsze jest spełnione.
Obszary rozciąganych prętów rzeczywistych, gdzie nie jest spełnione
zało enie o równomierności naprę eń normalnych
(Zb.Brzoska, Wytrzymałość Materiałów, PWN Warszawa 1979)
- 1/ 9 -
2. Rozciąganie (ściskanie) pręta
2.1. Analiza wytrzymałościowa pręta rozciąganego (ściskanego)
Zało enia:
− pręt jest prosty,
− pręt obcią ony jest siłami działającymi osiowo:
o skupionymi Pi [N],
o rozło onymi w sposób ciągły qi [N/m],
− pręt znajduje się w równowadze,
− pręt mo e posiadać zmienne pole powierzchni przekroju poprzecznego
(skokowo lub w sposób ciągły),
− pręt mo e być odcinkami zbudowany z ró nych materiałów.
y
qi
Pi
x
Pełna analiza wytrzymałościowa obejmuje:
1. wyznaczenie funkcji siły normalnej N(x)
na podstawie analizy równowagi myślowo odciętej części,
2. wyznaczenie funkcji naprę eń normalnych σ(x),
σ (x ) =
N (x )
S (x )
S(x) – pole powierzchni przekroju poprzecznego pręta w miejscu
określonym współrzędną x,
3. wyznaczenie funkcji wydłu enia względnego ε(x)
z prawa Hooke’a
ε (x ) =
σ (x )
E (x )
E – moduł Younga materiału,
4. wyznaczenie funkcji przemieszczenia przekrojów u(x)
x
u (x ) = ∫ ε (x )dx
0
- 2/ 9 -
2. Rozciąganie (ściskanie) pręta
Przykład
Wykonać pełną analizę wytrzymałościową pręta OA o długości l, polu przekroju poprzecznego S, gęstości materiału ρ, zawieszonego
pionowo i obcią onego własnym cię arem. Moduł Younga materiału pręta równy jest E.
Dane: l=100m, S=1cm2, ρ=7850kg/m3, E=2.1⋅105MPa, g≈10m/s2.
G/S=
=7.7MPa
G=770N N(x)
y
G/(SE)=
=3.67⋅10-5
σ(x)
u(x)
ε(x)
O
ρ, S, E
l
x
x
α
α
α
l-x
N(x)=G(x)
G (x ) l − x
=
G
l
⇓
G(x ) = G
cię ar pręta
N (x )
S
ε (x ) =
σ (x )
E
G(x)
A
x
σ (x ) =
α
l
l
x
l
x
l
x
1 G
l = 1.84mm
2 SE
x
x
u ( x ) = ∫ ε ( x )dx =
l−x
l
0
x
=
G = lSρg
G=100m⋅10-4m2⋅7850kg/m3⋅9.81m/s2=770N
G l−x
dx =
l
∫ SE
0
G
x2
x −
=
SE
2l
- 3/ 9 -
2. Rozciąganie (ściskanie) pręta
2.2. Energia odkształcenia przy rozciąganiu
Zało enia:
− siła rozciągająca narasta od
zera do swojej maksymalnej
wartości F
− spełnione jest prawo Hooke’a
L
S
L
∆L
F
F
siła rozciągająca
F
Energia odkształcenia U zgromadzona
w pręcie równa jest pracy W siły F
W
U =W =
wydłu enie
bezwzględne
1
F ⋅ ∆L [J ]
2
∆L
Energia odkształcenia na jednostkę objętości
Uv =
U
1 F ∆L 1
=
= σ ⋅ ε J / m3
LS 2 S L
2
po uwzględnieniu prawa Hooke’a
[
ε=
]
σ
E
1σ2 1 2
Uv =
= Eε J / m3
2 E 2
[
]
Energia odkształcenia na jednostkę masy
U
1
1 σ2
1
Um =
=
σ ⋅ε =
=
Eε 2 [J / kg ]
ρLS 2 ρ
2ρ
(…)
…
[
]
Energia odkształcenia na jednostkę masy
U
1
1 σ2
1
Um =
=
σ ⋅ε =
=
Eε 2 [J / kg ]
ρLS 2 ρ
2ρ E 2ρ
ρ - gęstość materiału pręta
- 4/ 9 -
2. Rozciąganie (ściskanie) pręta
2.3. Współczynnik bezpieczeństwa
Naprę enia w adnym miejscu konstrukcji
nie mogą przekroczyć dopuszczalnych wartości kr
(metoda naprę eń dopuszczalnych)
σmax ≤ kr
σ
σ
Rm
Re
ε
ε
przykładowy wykres rozciągania
dla materiału plastycznego
przykładowy wykres rozciągania
dla materiału kruchego
Re – granica plastyczności
Rm – wytrzymałość na rozciąganie
kr =
Re
ne
kr =
Rm
nm
współczynnik bezpieczeństwa
ne, nm >1
Wartość współczynnika bezpieczeństwa przyjmuje się w zale ności od:
− dokładności, z jaką znane są obcią enia zewnętrzne,
− charakteru obcią eń (stałe, zmienne),
− jakości technologii,
− warunków u ytkowania,
− dokładności danych…
… = sin γ α
dla małych kątów
sin γ α = γ α
γ α = 2ε (1 + ν ) sin α cos α
z prawa Hooke'a
ε=
σo
E
kąt odkształcenia postaciowego
γα =
2(1 + ν )
σ o sin α cos α
E
wydłu enie względne na kierunku α εα =
OA1 − a
a
ε α = ε (cos 2 α − ν sin 2 α )
wydłu enie względne na kierunku α−π/2 ε α −π / 2 =
OD1 − a
a
ε α −π / 2 = ε (sin 2 α − ν cos 2 α )
- 9/ 9 -
…
... zobacz całą notatkę






Komentarze użytkowników (0)