To tylko jedna z 26 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


4. Zginanie pręta
4. ZGINANIE PRĘTA
4.1. Wielkości charakteryzujące geometrię przekroju
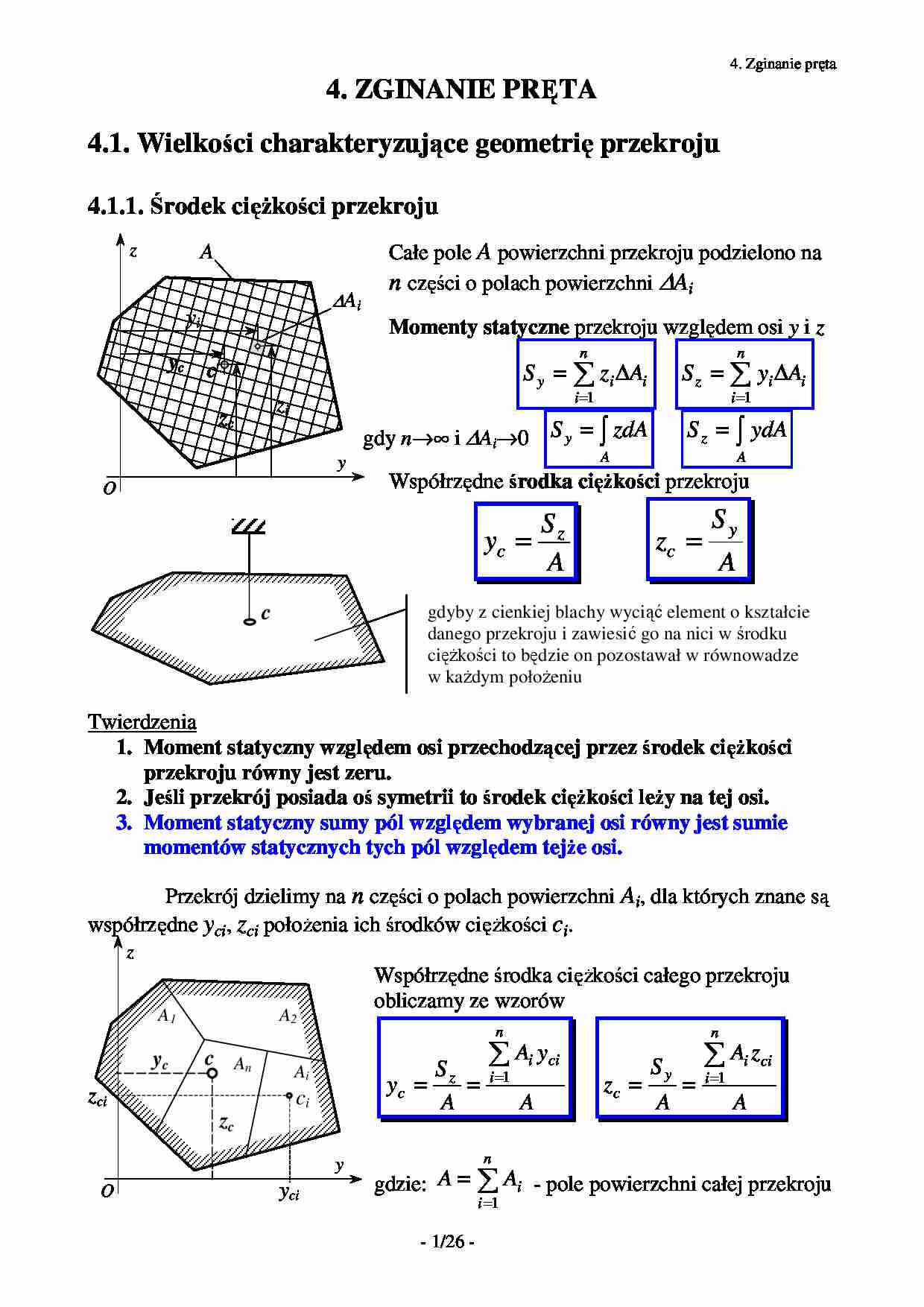
4.1.1. Środek cię kości przekroju
z
A
∆Ai
yi
yc
Całe pole A powierzchni przekroju podzielono na
n części o polach powierzchni ∆Ai
Momenty statyczne przekroju względem osi y i z
n
n
S y = ∑ zi ∆Ai
zi
zc
S z = ∑ yi ∆Ai
i =1
c
i =1
gdy n→∞ i ∆Ai→0 S y = ∫ zdA
S z = ∫ ydA
A
y
A
Współrzędne środka cię kości przekroju
O
S
yc = z
A
c
zc =
Sy
A
gdyby z cienkiej blachy wyciąć element o kształcie
danego przekroju i zawiesić go na nici w środku
cię kości to będzie on pozostawał w równowadze
w ka dym poło eniu
Twierdzenia
1. Moment statyczny względem osi przechodzącej przez środek cię kości
przekroju równy jest zeru.
2. Jeśli przekrój posiada oś symetrii to środek cię kości le y na tej osi.
3. Moment statyczny sumy pól względem wybranej osi równy jest sumie
momentów statycznych tych pól względem tej e osi.
Przekrój dzielimy na n części o polach powierzchni Ai, dla których znane są
współrzędne yci, zci poło enia ich środków cię kości ci.
z
A1
Współrzędne środka cię kości całego przekroju
obliczamy ze wzorów
A2
n
yc
c An
zci
S
yc = z =
A
Ai
ci
zc
y
O
yci
n
∑ Ai y ci
i =1
A
n
zc =
Sy
A
∑ Ai zci
=
i =1
A
gdzie: A = ∑ Ai - pole powierzchni całej przekroju
i =1
- 1/26 -
4. Zginanie pręta
Poło enie środka cię kości wybranych figur
prostokąt
c
b
a
trapez
h
c
b
trójkąt
a
a
h
c
h/3
b
wycinek pierścienia
R
r
2
c
rc =
2 R + Rr + r
3
R+r
α
2
sin
α
2
α [rad]
α
2
rc
przypadki szczególne
π
α=π/2
R
π
α=π/2
R
r=0
c
c
r
4R
3π
rc
rc
4 2 R 2 + Rr + r 2
rc =
3π
R+r
rc =
- 2/26 -
4 2
R
3π
4. Zginanie pręta
Przykład:
Wyznaczyć współrzędne środka cię kości przekroju ABCDEFGH pokazanego na
rysunku (wymiary podano w mm).
z
H
G
Kolejność postępowania:
1) obieramy układ współrzędnych y,z,
E
F
2) dzielimy przekrój na części, których
współrzędne środków cię kości mo na
łatwo obliczyć,
50
c(11.67, 21.67)
3) numerujemy te części od 1 do n,
4) przygotowujemy tabelkę według
D
C
podanego ni ej wzoru,
3
15
5) do tabelki wpisujemy pola powierzchni Ai
y
kolejnych części oraz współrzędne yci, zci
A 10
B
ich środków cię kości,
6) wykonujemy obliczenia w tabeli (kolumny
30
5 i 6),
7) kolumny 2, 5 i 6 podsumowujemy,
8) obliczamy współrzędne środka cię kości całego przekroju według podanych
wzorów, poło enie środka cię kości nanosimy na rysunku.
1
2
5
yci
zci
Aiyci
[mm ]
[mm]
[mm]
[mm ]
[mm3]
1
2
3
4
5
6
1
2
3
Σ
100
500
300
900
20
5
20
47.5
25
7.5
2000
2500
6000
10500
4750
12500
2250
19500
i
Ai
2
3
Aizci
yc=10500/900≅11.67mm zc=19500/900≅21.67mm
Metoda „pól ujemnych”
Rozpatrywany przekrój mo emy potraktować jako zło ony z dwóch figur:
1 – prostokąta ABGH, 2 – prostokąta CDEF ale o polu ujemnym.
yci
zci
Aiyci
[mm ]
[mm]
[mm]
[mm ]
[mm3]
1
2
3
4
5
6
1
2
Σ
1500
– 600
900
15
20
25
30
22500
–12000
10500
37500
–18000
19500
i
Ai
2
3
Aizci
yc=10500/900≅11.67mm zc=19500/900≅21.67mm
-
(…)
… w miejscu określonym
współrzędną x
qi(x)
z
Pi
Mgi
α
x
A
α
RA
B
RB
x
3. wyznaczyć siły wewnętrzne Mg(x), T(x) z warunków równowagi lewej lub
prawej myślowo odciętej części
qi(x)
z
α
Mg(x)
A
RA
T(x)
α
Mgi
T(x)
x
B
Mg(x)
α
α
x
Pi
x
- 14/26 -
RB
4. Zginanie pręta
Przykład:
Wykonać wykres momentów gnących Mg(x) oraz sił tnących T(x) dla belki pokazanej na rysunku.
z
q
Mg
x
A
C
B
E
D
P
l1
l2
l3
l4
l1=1m
l2=1m
l3…
…]
6.25
2.25
A
B
C
E
x
D
−6
−10
16
Mg [kNm]
7.5
6.25
1.25
A
B
x
C
D
E
Otrzymane wykresy sił wewnętrznych stanowią podstawę dalszej analizy
wytrzymałościowej belki.
- 17/26 -
4. Zginanie pręta
4.4. Odkształcenia i naprę enia przy czystym zginaniu belki
pryzmatycznej
Czyste zginanie – taki sposób obcią enia belki, e w przekrojach na pewnym jej
odcinku panuje jedynie moment gnący Mg (siła tnąca T=0…
… – a zatem
wzajemne działanie naprę eń stycznych i normalnych „sumuje się” w bardzo małym
stopniu.
T
P
d
T=
P
τ max =
sworzeń
kt – naprę
P
2
8 P
≤ kt
2
3 πd
P
T
enia dopuszczalne na ścinanie
Przykład konstrukcji, w której naprę enia styczne pełnią rolę dominującą
(połączenie sworzniowe)
- 23/26 -
4. Zginanie pręta
4.6. Zginanie ukośne
Zginanie ukośne − przypadek zginania belki, w którym wypadkowy moment…
… działania momentu gnącego Mg do płaszczyzny x-y
M gz
M g sinα
M
M cos α
σ 1 = − gy z = − g
z
σ2 = −
y=−
y
σ =σ1 +σ2 = −
Jy
M g cos α
Jy
- 24/26 -
Jz
z−
Mgz
x
zginanie
momentem Mg
Jy
y
M g sin α
Jz
y
Jz
4. Zginanie pręta
z
Równanie osi obojętnej (σ=0)
−
β
Jy
z−
z = −y
Mg
M g sin α
Jz
⇓
y
α
c
M g cosα
Jy
Jz
y =0
tg α
x
oś obojętna
przekroju
tg β = −
Jy
Jz
tg α
Oś obojętna przy zginaniu ukośnym przechodzi…
…=10500/900≅11.67mm zc=19500/900≅21.67mm
- 3/26 -
4. Zginanie pręta
4.1.2. Momenty bezwładności przekroju
z
Całe pole A powierzchni przekroju podzielono na
n części o polach powierzchni ∆Ai
A
∆Ai
yi
Momenty bezwładności względem osi
gdy n→∞ i ∆Ai→0
J y = ∑ zi2 ∆Ai
n
i =1
A
n
ri
J y = ∫ z 2 dA
J z = ∫ y 2 dA
i =1
A
zi
y
J z = ∑ yi2 ∆Ai
O
Biegunowy moment bezwładności
gdy n→∞ i ∆Ai→0
J O = ∫ r 2 dA =
n
J…
... zobacz całą notatkę






Komentarze użytkowników (0)