To tylko jedna z 21 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


STATYKA PŁYNÓW
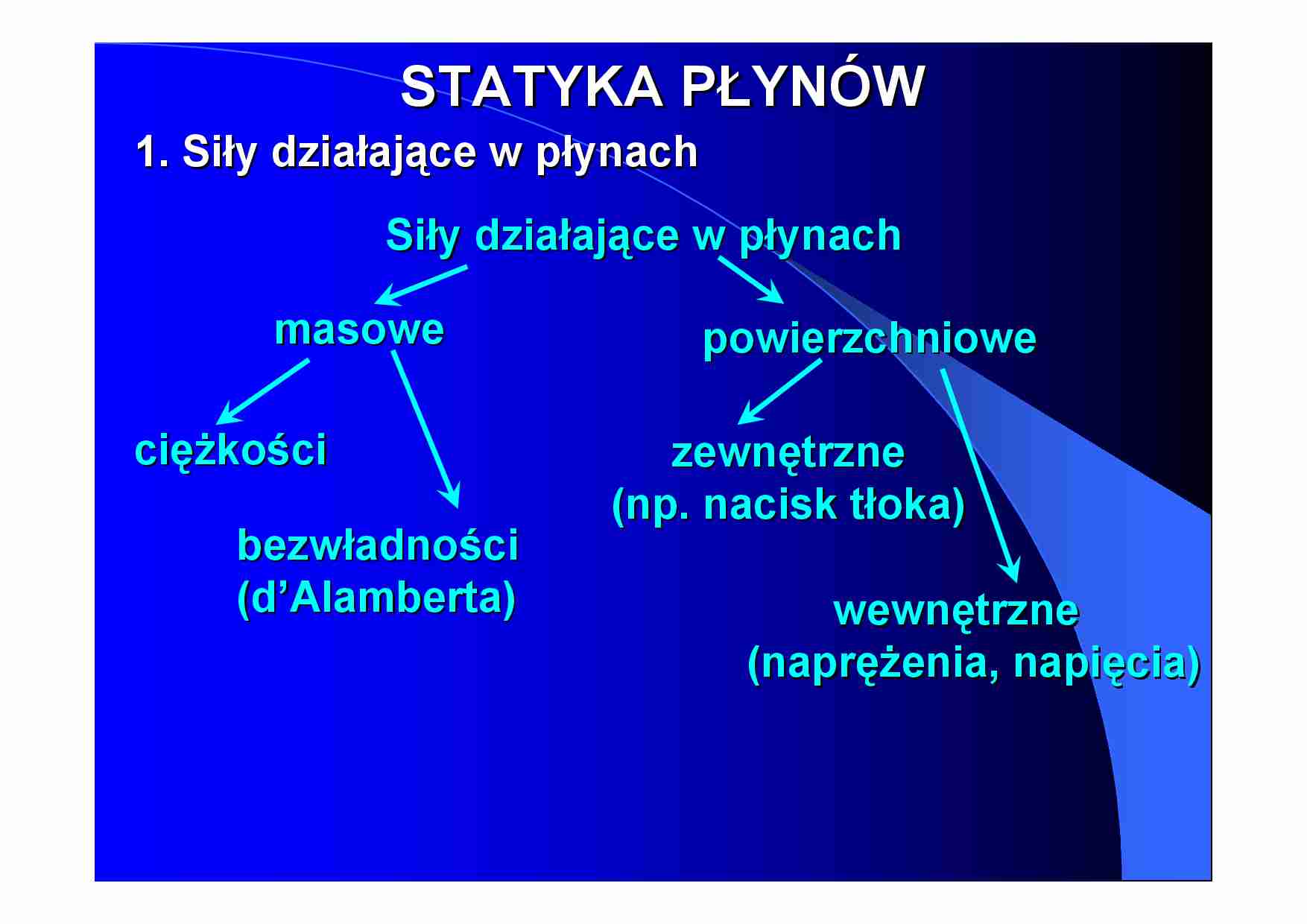
1. Siły działające w płynach
Siły działające w płynach
masowe
ciężkości
bezwładności
(d’Alamberta)
powierzchniowe
zewnętrzne
(np. nacisk tłoka)
wewnętrzne
(naprężenia, napięcia)
Siły masowe działają wówczas, gdy płyn znajduje się w polu
sił (ciężkości, bezwładności). Cechą charakterystyczną tych
sił jest to, że działają one na wszystkie cząstki
rozpatrywanej objętości płynu.
A(t )
( x, y , z )
∆Q
V (t )
∆M
Jednostkową siłę masową definiujemy w postaci:
∆Q
q = lim
= iX + jY + kZ
∆M → 0 ∆ M
gdzie: q ( X , Y , Z ) ,
∆Q - jest wektorem głównym sił masowych.
n
∆A
σ
Siły powierzchniowe σ definiujemy w postaci:
∆P
σ = lim
∆A → 0 ∆ A
(
W ogólnym przypadku σ = σ x, y , z , t , nx , n y , nz
)
2. Rodzaje ciśnień
Ciśnienie absolutne p1 – ciśnienie mierzone względem
absolutnej próżni.
P
pn + pb
pn
pb
pw
pb + pw
p1
0
Ciśnienie względne – ciśnienie mierzone względem innego
ciśnienia.
Nadciśnienie pn – nadwyżka ciśnienia absolutnego p1 nad
ciśnieniem barometrycznym pb.
pn = p1 - pb
Podciśnienie pw – różnica pomiędzy ciśnieniem
barometrycznym pb i ciśnieniem absolutnym p2
mniejszym niż pb.
pw = pb – p2
3. Równania równowagi płynów
Siły masowe i powierzchniowe działające na element płynu
1 ∂p ⎞
1 ∂p ⎞
∂p
⎛
⎛
dx ⎟ dydz − ⎜ p +
dx ⎟ dydz = − dxdydz
⎜ p−
2 ∂x ⎠
2 ∂x ⎠
∂x
⎝
⎝
⎛
⎛
∂p
1 ∂p ⎞
1 ∂p ⎞
dy ⎟ dxdz − ⎜ p +
dy ⎟ dxdz = − dxdydz
⎜ p−
∂y
2 ∂y ⎠
2 ∂y ⎠
⎝
⎝
∂p
1 ∂p ⎞
1 ∂p ⎞
⎛
⎛
p−
dz ⎟ dxdy − ⎜ p +
dz ⎟ dxdy = − dxdydz
⎜
∂z
2 ∂z ⎠
2 ∂z ⎠
⎝
⎝
∂p
dxdydz = 0
∂x
∂p
ρYdxdydz − dxdydz = 0
∂y
∂p
ρ Zdxdydz − dxdydz = 0
∂z
ρ Xdxdydz −
( 4)
( 5)
(6)
mnożymy równania obustronnie przez dx, dy, dz
∂p
ρ X = | dx
∂x
∂p
ρY = | dy
∂y
(7)
∂p
ρ Z = | dz
∂z
(9)
∂p
∂p
∂p
ρ Xdx + ρYdy + ρ Zdz = dx + dy + dz
∂x
∂y
∂z
(8)
(10 )
Dla dp=0 otrzymamy równanie powierzchni
jednakowego ciśnienia:
Xdx + Ydy + Zdz = 0
(11)
Prawo Pascala
Równania (7-9) w formie wektorowej mają postać:
ρ q = grad p
gdzie q jest wektorem jednostkowej siły masowej o
składowych X,Y,Z. W przypadku gdy na płyn nie działają
siły masowe (q=0) równanie to przybiera postać:
grad p = 0
p = const
czyli:
Stanowiące prawo Pascala.
Prawo Pascala – gdyby na płyn działały siły wyłącznie
powierzchniowe, to ciśnienie miało by jednakową
wartość w każdym punkcie płynu. Brak sił masowych
oznacza, że płyn jest nieważki. Ten warunek spełniony
jest w przybliżeniu dla gazów. Prawo Pascala stosuje
się również dla cieczy, gdy płyn znajduje się pod
dużym ciśnieniem, np. w prasach hydraulicznych.
p1 p2
p=
=
A1 A2
4. Równowaga cieczy w polu sił ciężkości
zo
po
z
z
h
ρ
g
W polu sił ciężkości składowe jednostkowej siły masowej
wynoszą:
(12 )
X = 0, Y = 0, Z = g
Po podstawieniu do równania (11), równanie
powierzchni jednakowego ciśnienia przyjmuje postać:
gdz = 0 → z = const
Elementarny przyrost ciśnienia:
dp = ρ gdz → p = ρ gz + c
(13)
Stałą c wyznaczamy z warunku brzegowego:
zatem:
gdy z=z 0 to p=p 0 → c = p0 − ρ gz0 ,
p-p 0 = ρ g ( z − z0 ) = ρ gh.
Wielkość h =
(…)
… wyznaczamy z warunku brzegowego:
zatem:
gdy z=z 0 to p=p 0 → c = p0 − ρ gz0 ,
p-p 0 = ρ g ( z − z0 ) = ρ gh.
Wielkość h = ( p − p0 ) / ρ g
nazywamy wysokością
ciśnienia hydrostatycznego, p- p0 jest ciśnieniem
hydrostatycznym
(14 )
5. Naczynia połączone
Prawo naczyń połączonych: Cząstki cieczy należące do tej
samej masy ciekłej, leżące na tej samej płaszczyźnie
poziomej, podlegają działaniu jednakowego…
... zobacz całą notatkę






Komentarze użytkowników (0)