To tylko jedna z 23 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
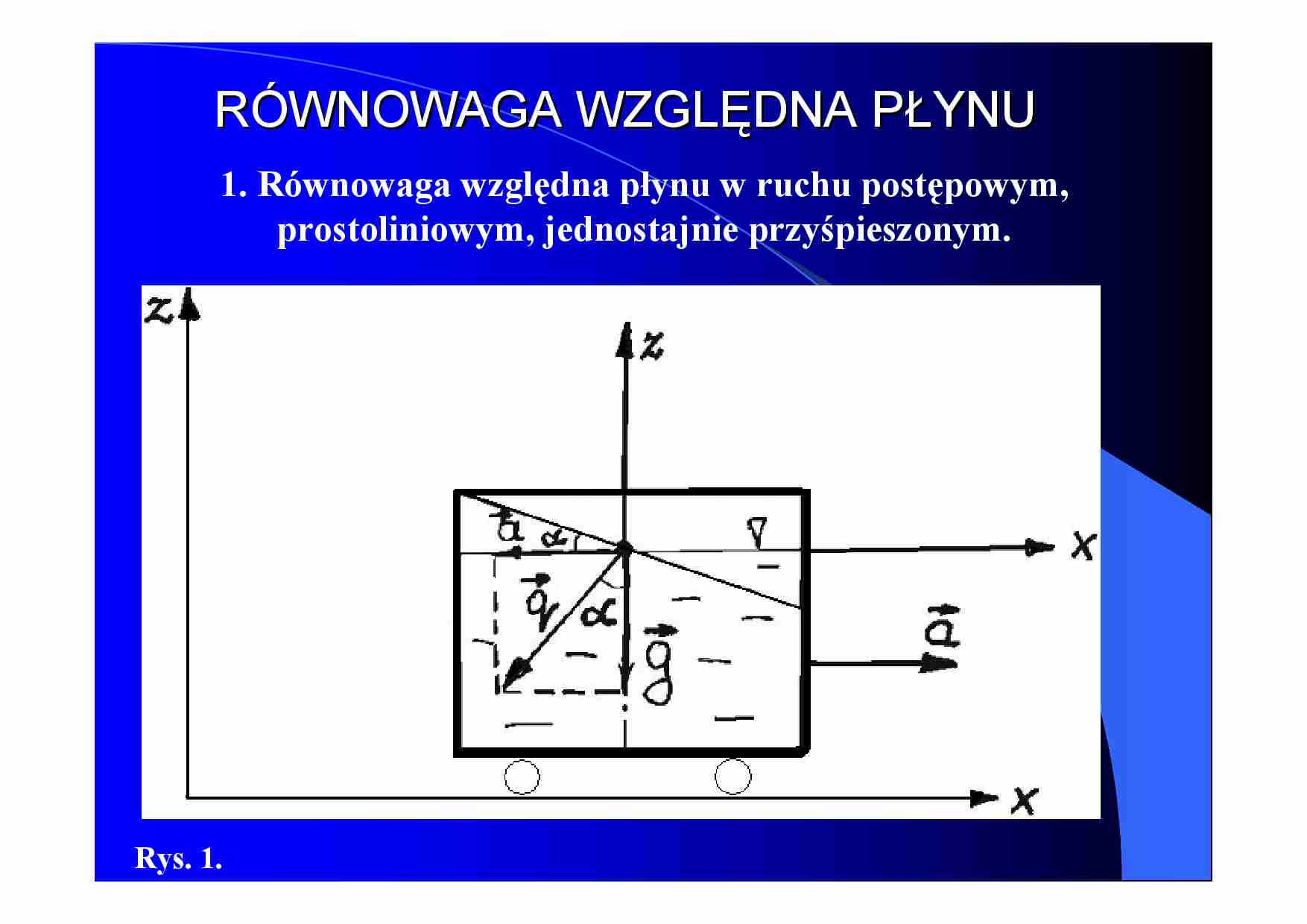


RÓWNOWAGA WZGLĘDNA PŁYNU
1. Równowaga względna płynu w ruchu postępowym,
prostoliniowym, jednostajnie przyśpieszonym.
Rys. 1.
Wyznaczamy powierzchnię jednakowego ciśnienia. Ogólnie równanie ma postać:
Xdx + Ydy + Zdz = 0.
(1)
Składowa jednostkowe siły masowej wynoszą:
X = −a, Y = 0, Z = −g.
(2)
Po podstawieniu (1) do (2) otrzymamy:
−adx − gdz = 0,
(3)
a po scałkowaniu
−ax + gz = c.
(4)
Po przekształceniu otrzymamy kierunkowe równanie płaszczyzny nachylonej
do poziomu pod kątem α , oznaczonym na rys. 1.
z=−
a
c
a
c
x − = − x + c1 , gdzie c1 = −
g
g
g
g
a
g
(5)
(6)
zatem tg α = .
Widać zatem, że w rozpatrywanym przypadku powierzchnie jednakowego
ciśnienia są płaszczyznami nachylonymi do poziomu pod kątem α .
Rozkład ciśnienia wyznaczamy z zależności
dp = ρ ( Xdx + Ydy + Zdz )
(7)
Która po podstawieniu wartości składowych jednostkowej siły masowej,
określonym równaniem (2) przybiera postać.
dp = −ρ ( adx + gdz ) .
(8)
Po scałkowaniu
p = −ρ ( ax + gz ) + c.
(9)
Stałą c wyznaczamy z warunku, że gdy x=0 i z=0, to p = pb , zatem c = pb .
Równanie (9) przybiera więc postać:
p = pb − ρ ( ax + gz )
(10)
2. Równowaga względna cieczy w ruchu jednostajnie obrotowym
wokół pionowej osi.
Rys. 2.
Składowe jednostkowe siły masowej wynoszą:
X = ω2x, Y = ω2y, Z = -g.
(11)
Po podstawieniu do równani (1) otrzymamy:
ω2xdx + ω2ydy − gdz = 0.
Po scałkowaniu
(12)
1 2 2 1 2 2
ω x + ω y − gz = c.
2
2
(13)
2
2
2
Ponieważ x + y = r , (rys. 2.), to równanie (13) przybiera postać
1 2 2
ω r − gz = c.
2
(14)
Równanie swobodnej powierzchni cieczy wyznaczamy dobierając stałą c tak,
aby dla r=0 współrzędna z = z0 . Stała c = −gz0 .
Po podstawieniu do(14) otrzymujemy równanie swobodnej powierzchni cieczy
w postaci
1 2 2
ωr
z − z0 =
(15)
2g
Jeśli naczynie w stanie spoczynku było wypełnione do wysokości h, to z0
wyznaczamy z porównania objętości
1
π R 2H
(16)
2
Dla r = R, z − z0 = H , zatem z równania (15) H = R 2ω 2 / 2g , więc równanie
(16) przybiera postać
1
π R 2h = π R 2z0 +
π R 4ω 2
(17)
4g
a współrzędna z0 = h − R 2ω 2 / 4g .
Po podstawieniu do (15) otrzymamy
1 2⎛ 2 1 2⎞
ω ⎜r − R ⎟ .
z =h+
(18)
2g
2 ⎠
⎝
π R 2h = π R 2z0 +
ROZKŁAD CIŚNIEŃ
Po podstawieniu (11) do (7) otrzymamy;
dp = ρω 2 ( xdx + ydy ) − ρ gdz.
(19)
Po scałkowaniu
p=
a po przekształceniu
1
ρω 2 x2 + y2 − ρ gz + c,
2
(
)
(20)
1
(21)
ρω 2r2 − ρ gz + c.
2
Stałą c wyznaczamy z warunku: r = 0, z − z0 , p=p0 to c=p0 + ρ gz0
i po podstawieniu jej do równania (21) otrzymamy równanie na rozkład
ciśnienia w postaci:
p=
p = p0 +
1
ρω 2r2 − ρ g ( z − z0 ) .
2
(22)
3. Równowaga względna płynu w ruchu jednostajnie obrotowym
wokół poziomej osi.
a) w naczyniu całkowicie wypełnionym cieczą
∆OO1M ∼ ∆MAB
OO1
g
g
=
→ OO1 = 2
r
ω
rω 2
Rys. 3.
Składowe jednostkowe siły masowej wynoszą:
X = ω 2x, Y=0, Z=ω 2z − g
(23)
Po podstawieniu do równania jednakowej powierzchni ciśnienia
Xdx+Ydy+Zdz=0 otrzymamy:
ω 2x dx + (ω 2z − g) dz = 0.
(24)
1 2 2 1 2 2
ω x + ω z − gz =
(…)
… obrotowy wokół pionowej osi. Przy jakiej
prędkości kątowej powierzchnia swobodna cieczy będzie styczna do ściany
zbiornika ?
Równanie swobodnej powierzchni cieczy ma postać:
r2ω 2
z − z0 =
,
2g
(1)
a po przekształceniu
r=
2g
ω
z − z0 .
(2)
Pochodna dr/dz wynosi
2g
dr
1
=
,
dz
2ω z − z0
a w punkcie z=H odpowiednio
⎞
2g ⎛
1
R
⎛ dr ⎞
⎜
⎟ = tgα = .
=
⎜ dz ⎟
2ω ⎜ H − z0 ⎟
H
⎝
⎠z = H
⎝
⎠
(3)
(4)
Równanie (1…
… + g sin α ) dz = 0.
2
2
2
Po scałkowaniu :
1 2 2
ω x + y2 + gx cos α sin α − gz cos2 α = c.
2
Powierzchnie jednakowego ciśnienia mają więc kształt paraboloid obrotowych
(
)
Przykład 4
Zamknięte naczynie cylindryczne o średnicy D i wysokości H wypełnione
jest cieczą do wysokości h. Przy jakiej prędkości kątowej paraboloidy
tworzącej powierzchnię swobodną dotknie dna.
a) Dla h<H/2
Równanie powierzchni…
… składowych siły masowej (23) do równania na rozkład
ciśnienia otrzymamy:
(
)
dp = ρ ⎡ω 2xdx + ω 2z − g dz ⎤
⎣
⎦
które po scałkowaniu przybiera postać
⎡1 2 2 1 2 2
⎤
p = ρ ⎢ ω x + ω z − gz ⎥ + c,
2
⎣2
⎦
lub
(27)
(28)
1
ρω 2r2 − ρ gz + c.
(29)
2
Gdy ω → ∞ to OO1 → 0 i powierzchnie ekwipotencjalne stają się walcami o
osi pokrywającej się z osią obrotu.Wzór na rozkład ciśnienia przybiera postać
p=
p = pp +
1
ρω…
... zobacz całą notatkę






Komentarze użytkowników (0)