To tylko jedna z 18 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


RÓWNANIA RUCHU PŁYNU
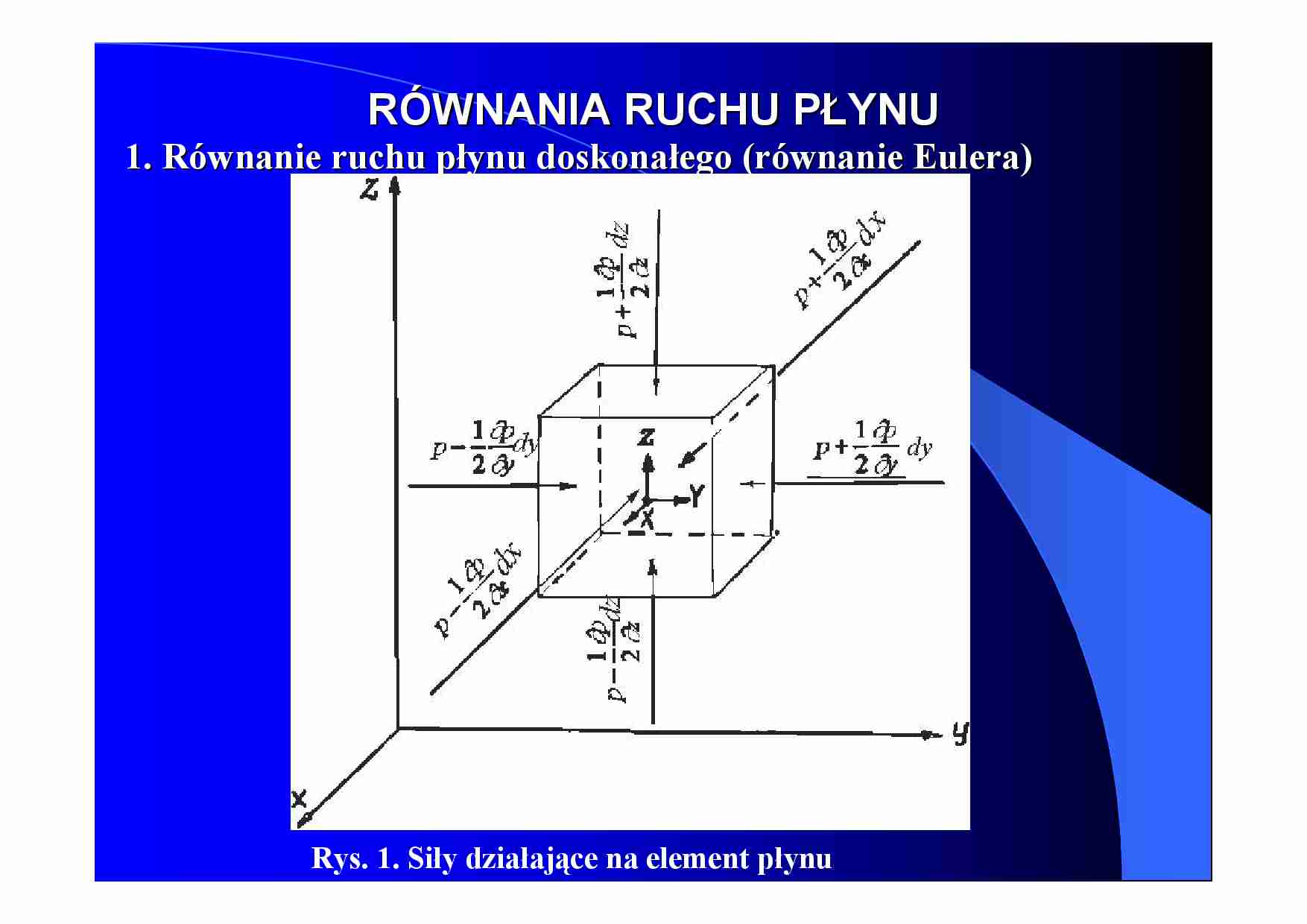
1. Równanie ruchu płynu doskonałego (równanie Eulera)
Rys. 1. Siły działające na element płynu
Wektor jednostkowej siły masowej q( X , Y , Z ) ma składowe X , Y , Z
a składowe siły masowej działającej na element płynu o gęstości ρ i
wymiarach dx, dy, dz wynoszą: ρXdxdydz, ρYdxdydz, ρZdxdydz.
Składowe sił powierzchniowych:
1 ∂p ⎞
1 ∂p ⎞
∂p
⎛
⎛
dx ⎟dydz = − dxdydz,
dx ⎟dydz − ⎜ p +
p−
⎜
2 ∂x ⎠
2 ∂x ⎠
∂x
⎝
⎝
⎛
⎛
1 ∂p ⎞
1 ∂p ⎞
∂p
⎜p−
dy ⎟dxdz − ⎜ p +
dy ⎟dxdz = − dxdydz,
⎟
⎜
⎜
2 ∂y ⎠
2 ∂y ⎟
∂y
⎠
⎝
⎝
1 ∂p ⎞
1 ∂p ⎞
∂p
⎛
⎛
p−
dz ⎟dxdy − ⎜ p +
dz ⎟dxdy = − dxdydz.
⎜
2 ∂z ⎠
2 ∂z ⎠
∂z
⎝
⎝
(1)
Składowe siły bezwładności − adm ,działającej na elementarną masę dm = ρdxdydx
wynoszą:
dν y
dν x
dν z
−
ρdxdydz,−
ρdxdydz,−
ρdxdydz.
dt
dt
dt
(2)
Zgodnie z zasadą d’Alamberta suma sił czynnych i sił bezwładności jest równa
zero, zatem:
dν x
∂p
Xρdxdydz − dxdydz −
ρdxdydz = 0,
∂x
dt
dν y
∂p
Yρdxdydz − dxdydz −
ρdxdydz = 0,
∂y
dt
∂p
dν z
Zρdxdydz − dxdydz −
ρdxdydz = 0.
∂z
dt
(3)
Po obustronnym podzieleniu przez ρdxdydz i przekształceniu
1 ∂p dν x
X−
=
,
ρ ∂x dt
1 ∂p dν y
Y−
=
,
dt
ρ ∂y
(4)
1 ∂p dν z
Z−
=
.
ρ ∂z
dt
W postaci wektorowej
dν
q − grad p =
.
ρ
dt
1
(5)
dν x dν y dν z
,
,
Rozwijając pochodne substancjalne
na pochodne lokalne
dt dt dt
i pochodne wędrowne otrzymamy:
∂ν x
∂ν x
∂ν x
1 ∂p ∂ν x
X−
=
+ν x
+ν y
+ν z
,
∂x
∂y
ρ ∂x ∂t
∂z
∂ν y
∂ν y
∂ν y
1 ∂p ∂ν y
Y−
=
+ν x
+ν y
+ν z
,
ρ ∂y ∂t
∂z
∂x
∂y
∂ν z
∂ν z
∂ν z
1 ∂p ∂ν z
Z−
=
+ν x
+ν y
+ν z
.
∂t
∂x
∂y
ρ ∂z
∂z
(6)
1.1 Równanie Eulera w funkcji składowych wektora wiru
Równanie Gromeko
Do prawej strony równań (6) dodamy i odejmiemy następujące wyrażenia:
⎛ ∂ν y
∂ν z ⎞
⎜
⎜ ∂x ν y + ∂x ν z ⎟
⎟
⎝
⎠
⎛ ∂ν z
∂ν x ⎞
⎜
⎜ ∂y ν z + ∂y ν x ⎟
⎟
⎝
⎠
∂ν y ⎞
⎛ ∂ν x
⎜
⎜ ∂z ν x + ∂z ν y ⎟
⎟
⎝
⎠
(6a)
Po przekształceniu otrzymamy układ równań w postaci:
∂ν x
∂ν x
1 ∂p ∂ν x ∂ν x
X−
νx +
νy +
νz
+
=
ρ ∂x ∂t
∂z
∂y
∂x
⎛ ∂ν y
∂ν z ⎞
∂ν z ⎞ ⎛ ∂ν y
+⎜
⎟
⎜ ∂x ν y + ∂x ν z ⎟ − ⎜ ∂x ν y + ∂x ν z ⎟ =
⎟ ⎜
⎠
⎝
⎠ ⎝
∂ν y
∂ν x ⎛ ∂ν x
∂ν z ⎞
+⎜
=
⎜ ∂x ν x + ∂x ν y + ∂x ν z ⎟
⎟
∂t ⎝
⎠
⎛ ∂ν y ∂ν x ⎞
⎛ ∂ν x ∂ν z ⎞
−
+ν z ⎜
⎟ −ν y ⎜
⎜ ∂x − ∂y ⎟.
⎟
∂x ⎠
⎝ ∂z
⎝
⎠
Analogiczne otrzymamy składowe w kierunku y,z:
∂ν y
∂ν z ⎞
1 ∂p ∂ν y ⎛ ∂ν x
Y−
=
+⎜
⎜ ∂y ν x + ∂y ν y + ∂y ν z ⎟
⎟
ρ ∂y ∂t ⎝
⎠
⎛ ∂ν y ∂ν x ⎞
⎛ ∂ν z ∂ν y ⎞
+ν x ⎜
⎜ ∂x − ∂y ⎟ −ν z ⎜ ∂y − ∂z ⎟,
⎜
⎟
⎟
⎝
⎝
⎠
⎠
(6b)
∂ν y
1 ∂p ∂ν z ⎛ ∂ν x
∂ν z ⎞
Z−
=
+⎜
⎜ ∂z ν x + ∂z ν y + ∂z ν z ⎟
⎟
ρ ∂z
∂t ⎝
⎠
⎛ ∂ν z ∂ν y ⎞
⎛ ∂ν x ∂ν z ⎞
+ν y ⎜
⎜ ∂y − ∂z ⎟ −ν x ⎜ ∂z − ∂x ⎟.
⎟
⎝
⎠
⎝
⎠
Z definicji wektora wiru jego składowe mają postać:
∂ν y ∂ν x
∂ν x ∂ν z
∂ν z ∂ν y
−
Wx =
−
,Wy =
−
, Wz =
.
∂x
∂y
∂y
∂x
∂z
∂z
(6c)
Po podstawieniu (6c) do (6b) otrzymamy:
∂ν y
∂ν z ⎞
1 ∂p ∂ν x ⎛ ∂ν x
+⎜
=
X−
⎜ ∂x ν x + ∂x ν y + ∂x ν z ⎟ +ν zWy −ν yWz ,
⎟
ρ ∂x ∂t ⎝
⎠
∂ν y
∂ν z ⎞
1 ∂p ∂ν y ⎛ ∂ν x
=
+⎜
Y−
⎜ ∂y ν x + ∂y ν y + ∂y ν z ⎟ +ν xWz −ν zWx ,
⎟
∂t ⎝
ρ ∂y
⎠
∂ν y
∂ν z ⎞
1 ∂p ∂ν z ⎛ ∂ν x
=
+⎜
Z−
⎜ ∂z ν x + ∂z ν y + ∂z ν z ⎟ +ν yWx −ν xW y .
⎟
∂t ⎝
ρ ∂z
⎠
Wyrażenia w
(…)
…
y
z
(6j)
Scałkujmy to równanie przy założeniu, że prawa strona jest równa zeru,
czyli:
⎛
p ν2 ⎞
d⎜ −U − − ⎟ = 0
⎜
ρ 2⎟
⎝
⎠
(6k)
Dla płynu nieściśliwego ( ρ = const ) otrzymamy równanie
p ν2
U+ +
= C = const
ρ 2
(6l)
a dla ściśliwego
p ν2
U +∫ +
= C = const
ρ 2
Zwane CAŁKĄ BERNOULLIEGO.
(6m)
W polu sił ciężkości o potencjale U = gz
otrzymamy dla płynu nieściśliwego
p ν2
gz + +
= C = const
ρ 2
(6n…
…. Ten warunek
będzie spełniony gdy:
a) gdy Wx = W y = Wz = 0 czyli w ruchu potencjalnym, ponieważ wówczas
,
stała C będzie jednakowym w całym obszarze płynącego płynu.
dx dy dz
=
=
b) Jeżeli
jest równaniem linii prądu
Wx W y W z
czyli w ruchu wirowym, ale tylko wzdłuż jednej linii wirowej; dla różnych linii
wirowych stała C będzie różna.
c) jeśli
dx
νx
=
dy
νy
=
dz
νz
jest równaniem linii prądu…
... zobacz całą notatkę






Komentarze użytkowników (0)