To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


1. RÓWNANIA RÓŻNICZKOWE RZĘDU PIERWSZEGO
1.1 POJĘCIA WSTĘPNE
Def. 1.1.1 (równanie różniczkowe zwyczajne pierwszego rzędu)
Równaniem różniczkowym zwyczajnym rzędu pierwszego nazywamy równanie postaci:
(R)
y' f (t , y) .
Uwaga. Będziemy się również posługiwali tzw. formą różniczkową równania różniczkowego, czyli równaniem postaci
P(t , y)dt Q(t , y)dy 0 .
Jednak najogólniejszą formą równania różniczkowego rzędu pierwszego jest równanie postaci
F (t , y, y' ) 0 .
Inaczej mówiąc równanie różniczkowe rzędu pierwszego jest zależnością między funkcją niewiadomą, zmienną niezależną i
pierwszą pochodną funkcji niewiadomej.
Def. 1.1.2 (rozwiązanie równania różniczkowego)
Funkcję y(t) nazywamy rozwiązaniem równania różniczkowego (R) na przedziale (a,b), jeżeli jest ona różniczkowalna na tym
przedziale oraz zamienia to równanie w tożsamość
y' (t ) f t , y(t ) ,
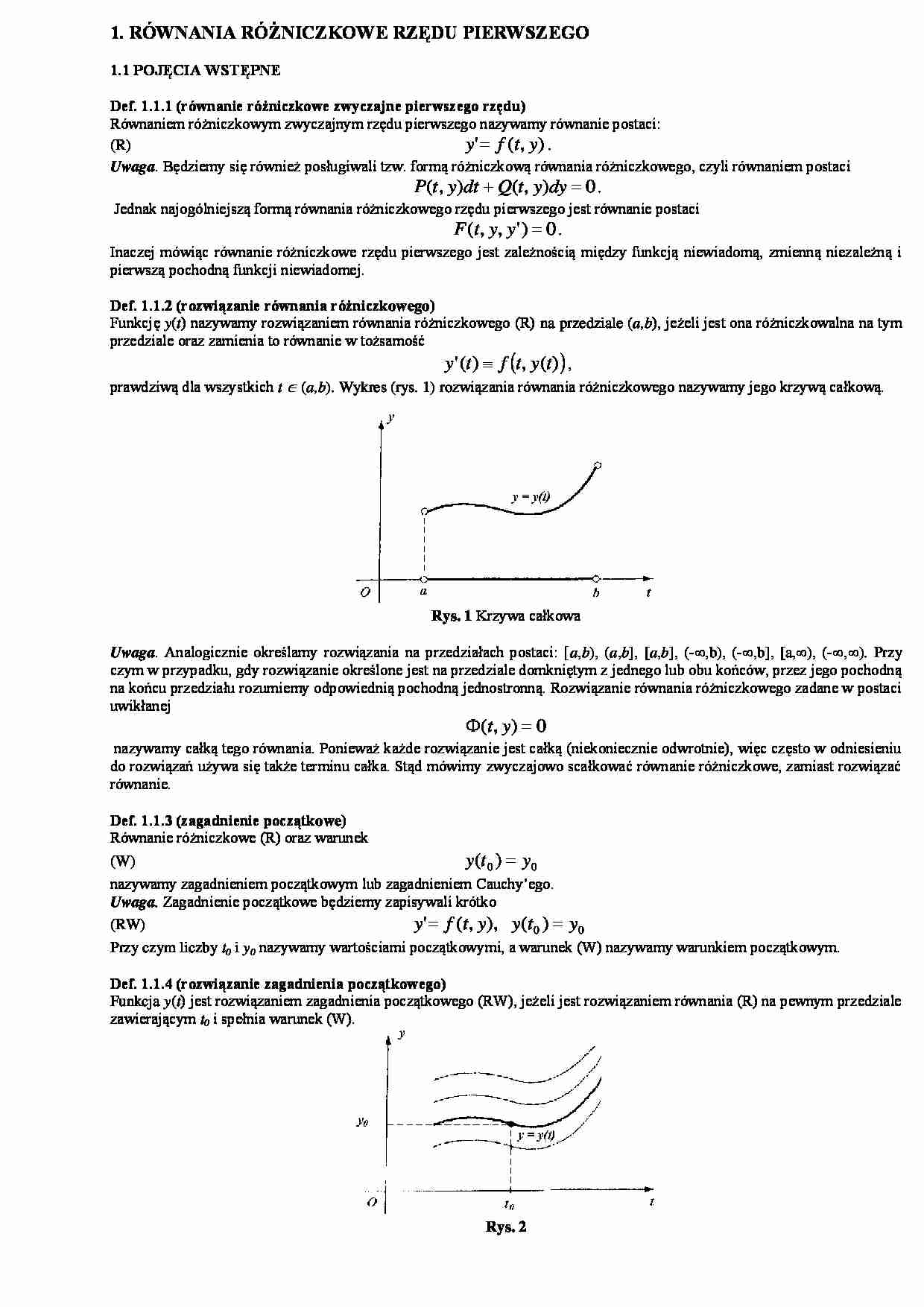
prawdziwą dla wszystkich t (a,b). Wykres (rys. 1) rozwiązania równania różniczkowego nazywamy jego krzywą całkową.
Rys. 1 Krzywa całkowa
Uwaga. Analogicznie określamy rozwiązania na przedziałach postaci: [a,b), (a,b], [a,b], (-,b), (-,b], [a,), (-,). Przy
czym w przypadku, gdy rozwiązanie określone jest na przedziale domkniętym z jednego lub obu końców, przez jego pochodną
na końcu przedziału rozumiemy odpowiednią pochodną jednostronną. Rozwiązanie równania różniczkowego zadane w postaci
uwikłanej
(t , y) 0
nazywamy całką tego równania. Ponieważ każde rozwiązanie jest całką (niekoniecznie odwrotnie), więc często w odniesieniu
do rozwiązań używa się także terminu całka. Stąd mówimy zwyczajowo scałkować równanie różniczkowe, zamiast rozwiązać
równanie.
Def. 1.1.3 (zagadnienie początkowe)
Równanie różniczkowe (R) oraz warunek
(W)
y(t 0 ) y 0
nazywamy zagadnieniem początkowym lub zagadnieniem Cauchy’ego.
Uwaga. Zagadnienie początkowe będziemy zapisywali krótko
y' f (t , y), y(t 0 )
(RW)
y0
Przy czym liczby t0 i y0 nazywamy wartościami początkowymi, a warunek (W) nazywamy warunkiem początkowym.
Def. 1.1.4 (rozwiązanie zagadnienia początkowego)
Funkcja y(t) jest rozwiązaniem zagadnienia początkowego (RW), jeżeli jest rozwiązaniem równania (R) na pewnym przedziale
zawierającym t0 i spełnia warunek (W).
Rys. 2
Uwaga. W interpretacji geometrycznej, rozwiązanie zagadnienia początkowego, polega na znalezieniu wśród wszystkich
krzywych całkowych równania (R) tej, która przechodzi przez punkt (t0,y0) (rys.2). Jednak zagadnienie to niekoniecznie musi
mieć jednoznaczne rozwiązanie. Może istnieć więcej niż jedno rozwiązanie danego zagadnienia początkowego. Istnienie
rozwiązań zagadnienia początkowego oraz ich jednoznaczność jest jednym z głównych problemów teorii równań
różniczkowych zwyczajnych.
Tw. 1.1.5 (o istnieniu i jednoznaczności rozwiązań równania (R))
Niech funkcja f(t,y) oraz jej pochodna cząstkowa
f
będą określone i ciągłe na obszarze domkniętym D R2. Wtedy dla
y
każdego punktu (t0,y0) D, zagadnienie początkowe (RW) ma dokładnie jedno rozwiązanie.
Uwaga.
... zobacz całą notatkę






Komentarze użytkowników (0)