RÓWNANIA NAVIERA-STOKESA
DLA PŁYNU NIEŚCIŚLIWEGO
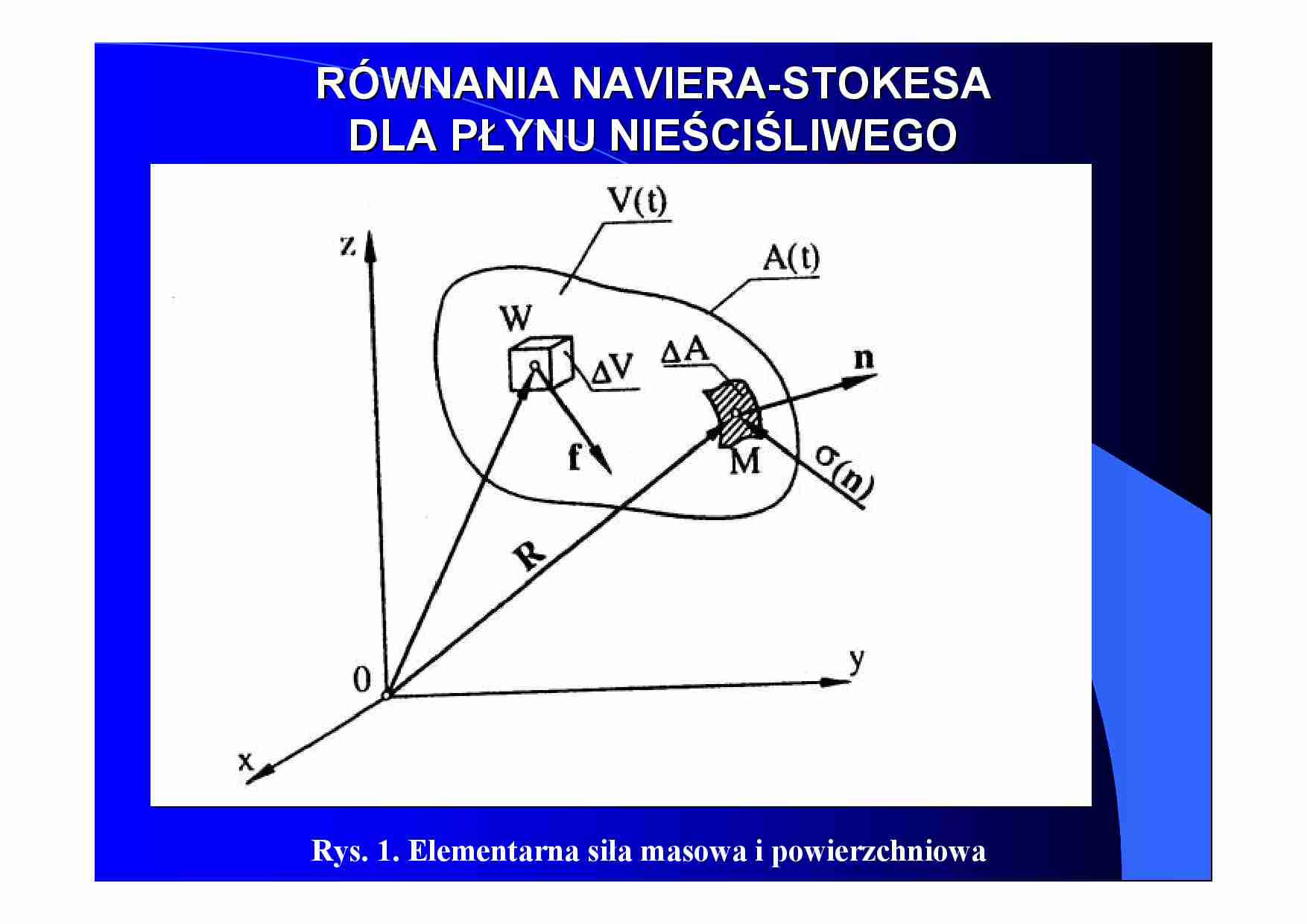
Rys. 1. Elementarna siła masowa i powierzchniowa
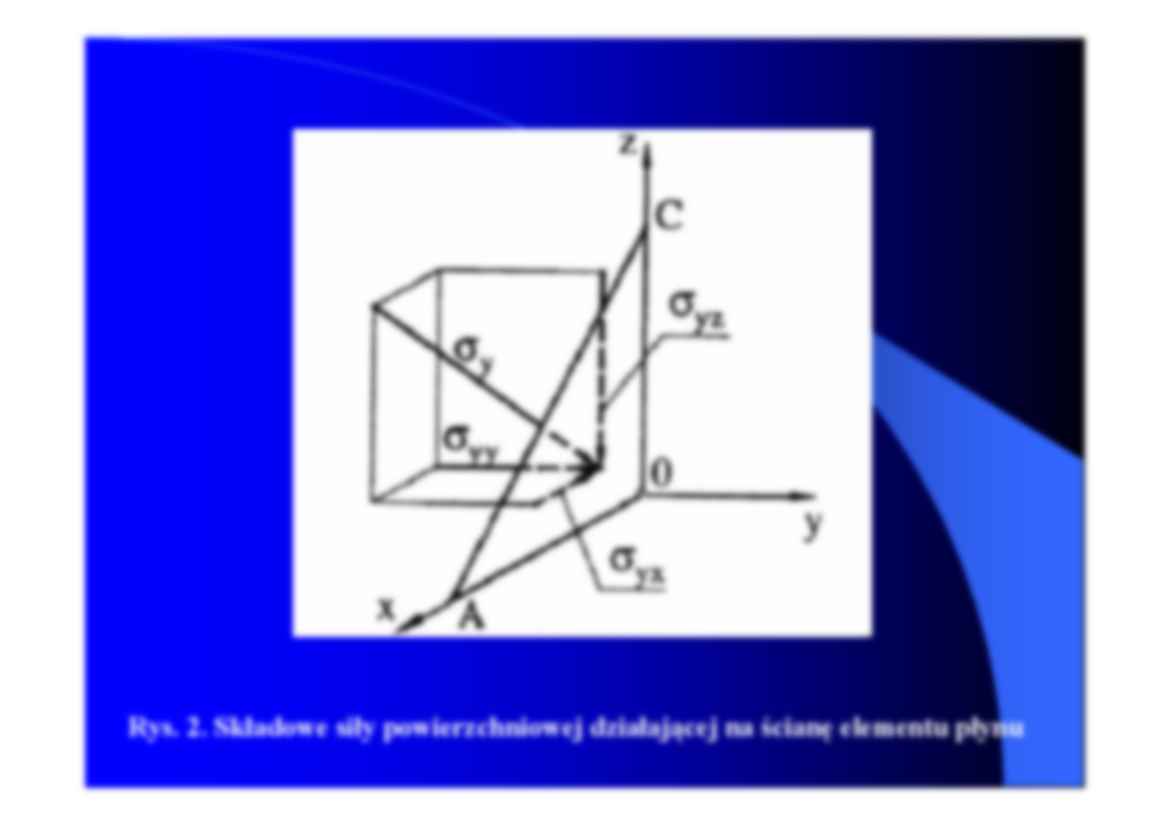
Rys. 2. Składowe siły powierzchniowej działającej na ścianę elementu płynu
W dalszej części składowe normalne będą nazywane ciśnieniami
(σ xx ≡ pxx ,σ yy ≡ p yy ,σ zz ≡ pzz ) a składowe o różnych wskaźnikach siłami
powierzchniowymi (naprężeniami) stycznymi ( σ yz ≡ τ yz , σ yx ≡ τ yx itp.)
Hydrodynamiczne równanie Eulera uzupełnimy składowymi jednostkowej siły
lepkości w postaci:
Fy'
Fx'
Fz'
Fx =
, Fy =
, Fz =
ρ dxdydz
ρ dxdydz
ρ dxdydz
gdzie:
Fx' , Fy' , Fz' są składowymi elementarnej, wypadkowej siły lepkości,
działającej na element płynu o wymiarach dx, dy, dz.
(1)
Po podstawieniu do równań Eulera otrzymamy
dν x
1 ∂p
− Fx =
X−
,
ρ ∂x
dt
dν y
1 ∂p
,
Y−
− Fy =
ρ ∂y
dt
1 ∂p
dν z
− Fz =
.
Z−
ρ ∂z
dt
(2)
Rys. 3. Rozkład jednostkowej siły powierzchniowej na trzy składowe
'
'
'
W celu wyznaczenia składowych Fx , Fy , Fz przeprowadzimy następującą
analizę. Wydzielimy elementarną powierzchnię dAx = dydz , leżącą w
płaszczyźnie yOz (rys. 1). Załóżmy, że w punkcie M działa jednostkowa siła
powierzchniowa (naprężenie) σ x . Rozłożymy ją na składową p xx normalną do
powierzchni dAx i na składowe styczne do tej powierzchni τ xy i τ xz wyniosą
odpowiednio:
Px = pxx dydz , Ty = τ xy dydz , Tz = τ xz dydz ,
(3)
Rys. 4. Jednostkowe siły powierzchniowe lepkości działające na ściany
sześciennego elementu płynu
Teraz wyznaczymy siły powierzchniowe (pochodzące od lepkości płynu)
działające na element płynu o wymiarach dx, dy, dz. Na rysunku 4 oznaczono
jednostkowe siły powierzchniowe, styczne i normalne działające na
poszczególne ściany elementu płynu. Pierwszym indeksem oznaczono
płaszczyznę normalną do osi układu współrzędnych a drugim kierunek
jednostkowej siły powierzchniowej.
Na płaszczyznach przyległych do wierzchołka A działają siły elementarne
W kierunku osi: Ox
p xx dydz,τ yx dxdz,τ zx dxdy,
Oy
p yy dxdz,τ xy dydz,τ zy dxdy,
Oz
p zz dxdy,τ xz dydz,τ yz dxdz,
(4)
Na płaszczyzny przyległe do wierzchołka C’ działają siły
W kierunku osi: Ox
'
'
'
p xx dydz,τ yx dxdz,τ zx dxdy,
Oy
'
'
p 'yy dxdz,τ xy dydz ,τ zy dxdy,
Oz
'
'
'
p zz dxdy,τ xz dydz,τ yz dxdz,
(5)
Przyrost na drodze dx, dy, dz, składowych w kierunku osi Ox wynoszą
odpowiednio:
'
p xx = p xx +
τ = τ yx +
'
yx
'
τ zx = τ zx +
∂p
dx,
∂x
∂τ yx
∂y
(6)
dy,
∂τ zx
dz,
∂z
Podobnie obliczamy przyrost składowych w kierunkach osi Oy i Oz.
'
Składowe siły elementarnej F wynoszą:
(
F = (p
F = (p
)
(
)dxdz + (τ
)dydz + (τ
)
(
)dydz + (τ
)dydz + (τ
)
)dxdy
)dxdz
'
'
'
Fx' = p xx − p xx dydz + τ yx − τ yx dxdz + τ zx − τ zx dxdy
'
y
− p 'yy
yy
'
z
'
− p zz
zz
'
− τ xy
xy
'
− τ zx
zx
'
− τ zy
zy
'
− τ yz
yz
(7)
Po podstawieniu zależności (6) otrzymamy
⎛ ∂p xx ∂τ yx ∂τ zx ⎞
F = −⎜
⎜ ∂x + ∂x + ∂z ⎟dxdydz
⎟
⎝
⎠
'
x
⎛ ∂p yy ∂τ xy ∂τ zy ⎞
F = −⎜
⎜ ∂y + ∂x + ∂z ⎟dxdydz
⎟
⎝
⎠
'
y
(8)
⎛ ∂p zz ∂τ xz ∂τ yz ⎞
F = −⎜
⎜ ∂z + ∂x + ∂y ⎟dxdydz
⎟
⎝
⎠
'
z
Naprężenia
(…)
… laminarny nazywamy więc
przepływem statecznym.
2. Przepływ płaski w szczelinie
Założenia
• płyn lepki nieściśliwy ρ = const , µ = const.
• pomijamy siły masowe q = 0.
• ruch ustalony
∂
= 0 laminarny, izotermiczny T
∂t
= const.
• przepływ odbywa się tylko w kierunku osi z (ν x = ν y = 0 ).
Podstawowe równania: równanie ciągłości (1) i Naviera-Stokesa (2),
div v = 0,
(1)
dv
q − grad p =
− υ∇ 2 v .
ρ
dt
(2)
1…
… równania w postaci
dυ x
1 ∂p
2
+ ν∇ υ x =
X−
ρ ∂x
dt
dυ y
1 ∂p
2
+ ν∇ υ y =
Y−
ρ ∂y
dt
Z−
(13)
1 ∂p
dυ
+ν∇ 2υ z = z
ρ ∂z
dt
w zapisie wektorowym równania (13) przybierają postać
dυ
q − grad p -ν∇ υ =
dt
ρ
1
2
(14)
SZCZEGÓLNE PRZEPŁYWY LAMINARNE
1. Rodzaje przepływów
1.1. Przepływ laminarny
W przepływie laminarnym cząstki płynu poruszają się po torach prostych
lub łagodnie zakrzywionych, narzuconych…
… prędkości w postaci:
1 ∆p
ν=
4 µl
(R
2
− r 2 ).
(23)
Maksymalna prędkość wystąpi dla r=0 , czyli w osi przewodu i wyniesie
ν max
1 ∆p 2
=
R.
4 µl
(24)
Strumień objętości wyznaczymy w następujący sposób:
dQ = 2πrdrν ,
π∆p R
Q=
r ( R 2 − r 2 )dr ,
2µl ∫
0
π∆p 4
Q=
R.
2µl
Zależność (27) wyraża prawo Hagena - Poisuille’a, będące związkiem
pomiędzy spadkiem ciśnienia i strumienia objętości.
(25)
(26)
(27…
... zobacz całą notatkę




Komentarze użytkowników (0)