To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Geometria wykreślna
Wykład 7
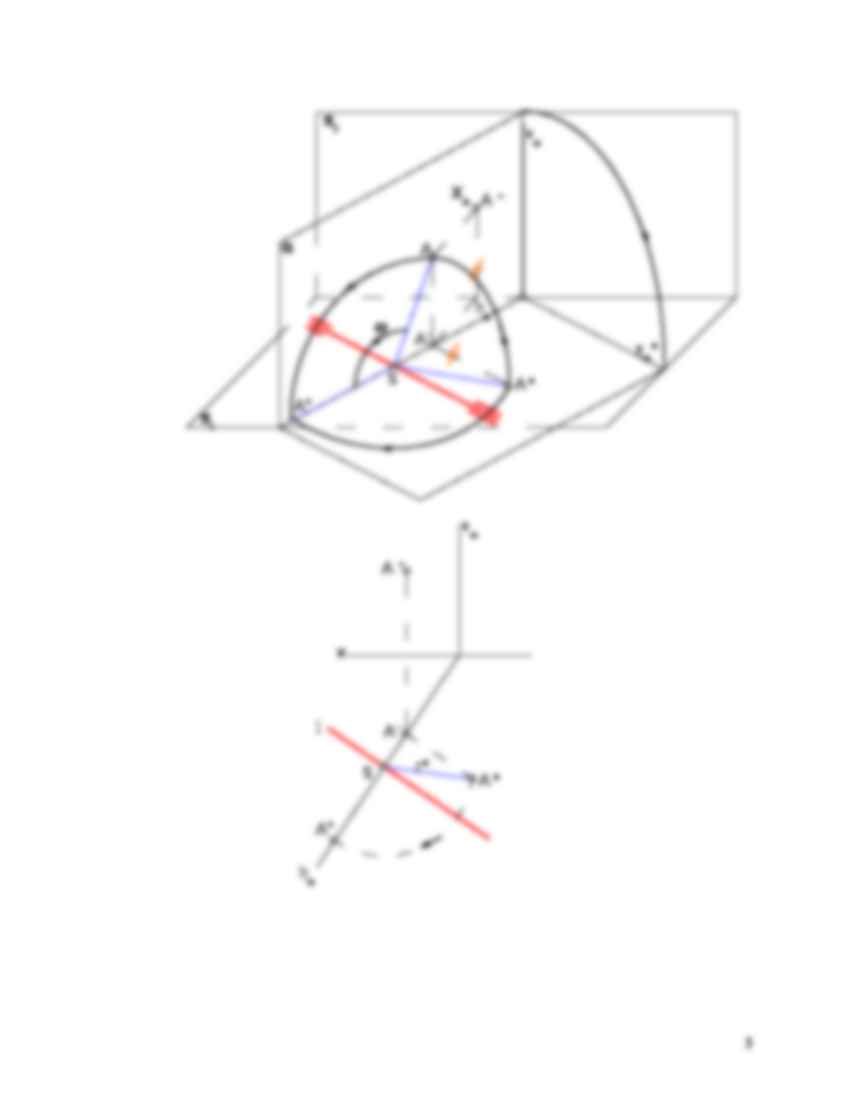
Obrót punktu wokół prostej
Obrotem punktu A wokół prostej l nazywamy przejście punktu A do nowego położenia Ao po łuku o promieniu równym odległości S.A., który leży na płaszczyźnie prostopadłej do prostej l. Prostą l nazywamy osią obrotu, płaszczyznę płaszczyzną obrotu, punkt S środkiem obrotu, a odległość AS promieniem obrotu. Rzeczywista długość odcinka wyznaczona metodą obrotu
Rzeczywista wielkość trójkąta wyznaczona metodą obrotu
Kład punktu
Kład punktu A wokół prostej l leżącej na którejś z rzutni nazywamy takie przekształcenie w którym punkt obracany jest na płaszczyźnie prostopadłej do prostej l o taki kąt aby po obrocie znalazł się na rzutni.
Kolejność postępowania:
Przez punkt A prowadzimy płaszczyznę prostopadła do niej. Płaszczyznę tę nazywamy płaszczyzną obrotu.
Punkt przecięcia S płaszczyzny i prostej l jest środkiem obrotu.
Dokonujemy kładu płaszczyzny na rzutnię 1. Odległość punktu S od kładu punktu A* jest promieniem obrotu.
Obracamy punkt A* o taki kąt aby znalazł się on na śladzie h Rzeczywista odległość między dwiema prostymi równoległymi
Zadania:
Wyznaczyć rzeczywistą długość odcinka AB metodą obrotu.
Wyznaczyć rzeczywistą wielkość trójkąta ABC leżącego na płaszczyźnie pionowo-rzutującej metodą obrotu.
Dane są rzuty trójkąta ABC leżącego na płaszczyźnie dowolnej. Wyznaczyć metodą obrotu kąt nachylenia tego trójkąta do rzutni poziomej oraz rzeczywistą wielkość tego trójkąta.
Wyznacz rzeczywistą odległość między dwiema prostymi równoległymi metodą kładu.
Wyznacz rzeczywistą odległość punktu P od prostej m metodą kładu.
Wyznacz rzeczywisty kąt między dwiema prostymi przecinającymi się metodą kładu. 1
Hn' Hn”
(…)
… rzeczywisty kąt między dwiema prostymi przecinającymi się metodą kładu. 1
Hn' Hn” Hm' Hm” n ” n' no m ” m' mo hα r* A ” A' x S Ao A* hα vα r* A ” A' x l S Ao A* S Ao A A ” A' vα*
π2 A* Xα hα vα π1
C2”
C2'
A2'
A2”
l2'
M”
M1'
B1'
B1”=l2”
M'
A1”
A1'
p1'
p”
p'
C”=M1”
C'=l1'
B”
B'
A”
A'
x
l1”
vε B'
Bo'
A'=S'=l'
A”
Bo”
S”
B”
x
ω l”
Ao'
l'=S'
A'
A”
Ao”
S”
π2 π1 Ao'
S'
A'
Ao S
A
A”
Ao”
S”
l
x
ω l”
…
... zobacz całą notatkę






Komentarze użytkowników (0)